Skip to main content

树的概念

基本概念​

树

树是一种非顺序数据结构, 前面所学的散列表也是一种非顺序数据结构.

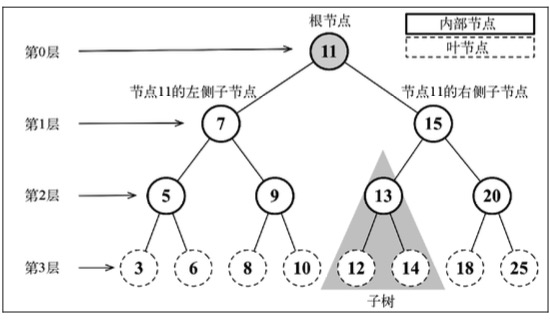
树的每个元素都称为节点, 当没有节点是称为空树, 节点分为内部节点和外部节点 (也叫叶子节点).

至少有一个子元素的节点称为内部节点, 如 7.

没有子元素的节点称为外部节点或叶子节点, 如 3.

位于树顶部的节点叫做根节点, 它是唯一一个没有父节点的节点.

子树由它的节点和它的后代构成, 如节点 13、12 和 14 构成了一棵子树.

节点有一个属性叫做深度, 它取决于该节点的祖先节点的数量, 如节点 3 有 3 个祖先 (5、7 和 11), 它的深度为 3.

树的高度取决于所有节点深度的最大值, 其中根节点高度值为 0, 因此图片中树的高度为 3.

节点与节点之间的关系称为边 (edge), 在图片中, 边可以认为是两个节点间的连线.

二叉树和二叉搜索树​

  • 二叉树: 最多有两个子节点, 一个是左侧子节点, 一个是右侧子节点.

  • 二叉搜索树(BST): 只允许在左侧存储比父节点小的值, 在右侧存储比父节点大的值, 开篇图就是一棵二叉搜索树.

几种特殊树​

222-count-nodes
中文名英文名解释
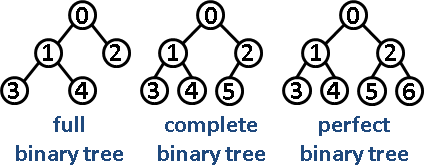
完美二叉树Perfect Binary TreeEvery node except the leaf nodes have two children and every level (last level too) is completely filled. 除了叶子结点之外的每一个结点都有两个孩子, 每一层(当然包含最后一层)都被完全填充.
完全二叉树Complete Binary TreeEvery level except the last level is completely filled and all the nodes are left justified. 除了最后一层之外的其他每一层都被完全填充, 并且所有结点都保持向左对齐.
完满二叉树Full/Strictly Binary TreeEvery node except the leaf nodes have two children. 除了叶子结点之外的每一个结点都有两个孩子结点.
  • 完美(Perfect)二叉树一定是完全(Complete)二叉树, 但完全(Complete)二叉树不一定是完美(Perfect)二叉树.
  • 完美(Perfect)二叉树一定是完满(Full)二叉树, 但完满(Full)二叉树不一定是完美(Perfect)二叉树.
  • 完全(Complete)二叉树可能是完满(Full)二叉树, 完满(Full)二叉树也可能是完全(Complete)二叉树.
  • 既是完全(Complete)二叉树又是完满(Full)二叉树也不一定就是完美(Perfect)二叉树.