Skip to main content

堆排序

概念​

堆排序是利用 heap 设计的一种排序算法, 堆排序是一种选择排序. 它的最坏, 最好, 平均时间复杂度均为 O(nlogn), 它是一种不稳定排序.

堆具有以下性质的完全二叉树: 每个结点的值都大于或等于其左右孩子结点的值, 称为大顶堆; 或者每个结点的值都小于或等于其左右孩子结点的值, 称为小顶堆.

按照下图的序号排列, 大顶堆得到一个从大到小排列的数组, 小顶堆得到一个从小到大排列的数组.

堆排序

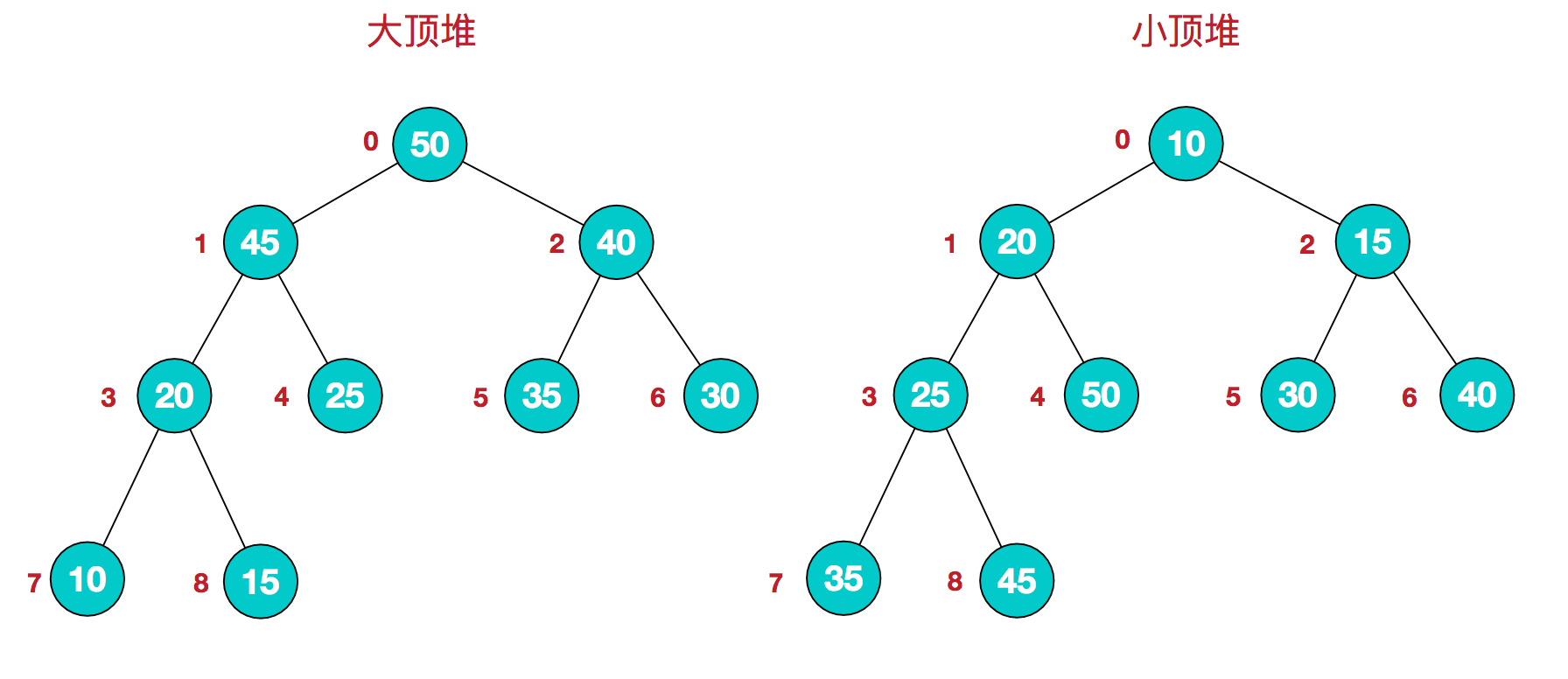
综合来讲:

大顶堆: arr[i] >= arr[2 * i + 1] && arr[i] >= arr[2 * i + 2]

小顶堆: arr[i] <= arr[2 * i + 1] && arr[i] <= arr[2 * i + 2]

实现​

若以升序排序说明, 把数组转换成最大堆(Max-Heap Heap), 这是一种满足最大堆性质(Max-Heap Property)的二叉树: 对于除了根之外的每个节点 i, A[parent(i)] >= A[i].

重复从最大堆取出数值最大的结点(把根结点和最后一个结点交换, 把交换后的最后一个结点移出堆), 并让残余的堆维持最大堆性质.

function swap(arr: number[], i: number, j: number) {
  const tmp = arr[i]
  arr[i] = arr[j]
  arr[j] = tmp
}

function maxHeapify(arr: number[], start: number, end: number) {
  // 建立父/子节点
  const dad = start
  let son = dad * 2 + 1
  if (son >= end)
    // 若子节点 > end 直接返回
    return
  if (son + 1 < end && arr[son] < arr[son + 1])
    // 先比较两个子节点大小, 选择最大的
    son++
  if (arr[dad] <= arr[son]) {
    // 如果父节点小于子节点时, 交换父子内容再继续子节点和孙节点比较
    swap(arr, dad, son)
    maxHeapify(arr, son, end)
  }
}

function heapSort(arr: number[]) {
  const len = arr.length
  // 初始化, 从最后一个父节点(非叶子结点)开始调整
  for (let i = Math.floor(len / 2) - 1; i >= 0; i--) {
    maxHeapify(arr, i, len)
  }

  // 先将第一个元素和已排好元素前一位做交换, 再重新调整, 直到排序完毕
  for (let i = len - 1; i > 0; i--) {
    swap(arr, 0, i)
    maxHeapify(arr, 0, i)
  }

  return arr
}

复杂度分析​

  • 平均时间复杂度: O(nlogn)
  • 空间复杂度: O(1)
  • 稳定性: 不稳定