Skip to main content

动态规划

从斐波那契数列说起​

朴素的斐波那契数列​

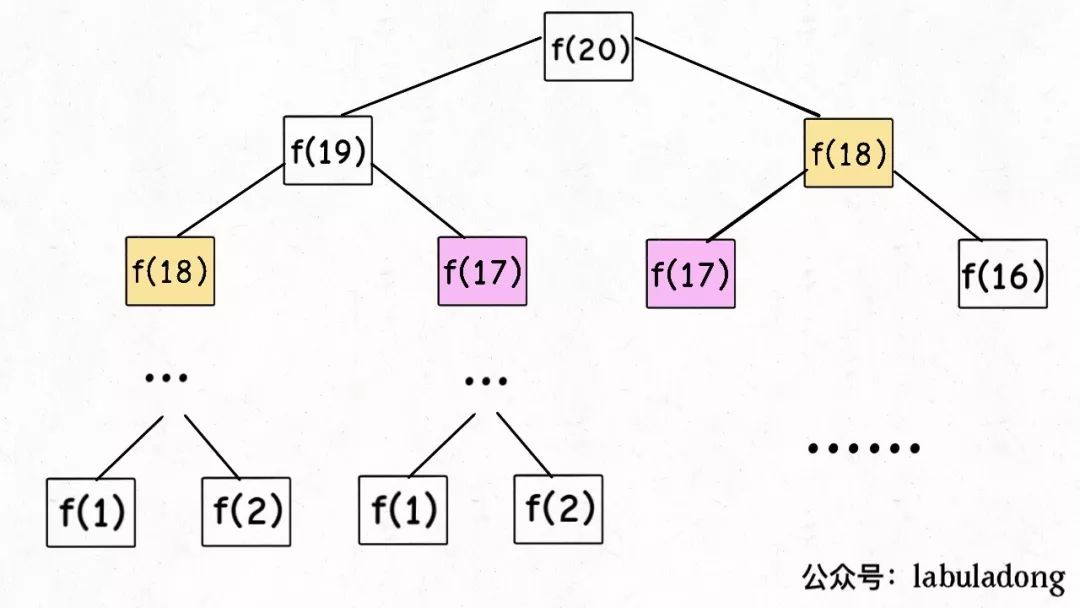
最暴力的递归大家都懂, 试了下 fibonacci1(100) 都卡成了狗, 原因在于大量数字被重复计算. 如下图所示, 像 f(18), f(17) 这些都被重复计算了一次, 此时时间复杂度到了 O(2n) 指数级别.

dynamic-programming

export const fibonacci1 = (n: number) => {
  if (n === 0 || n === 1) return n
  return fibonacci1(n - 1) + fibonacci1(n - 2)
}

使用"备忘录"的斐波那契数列​

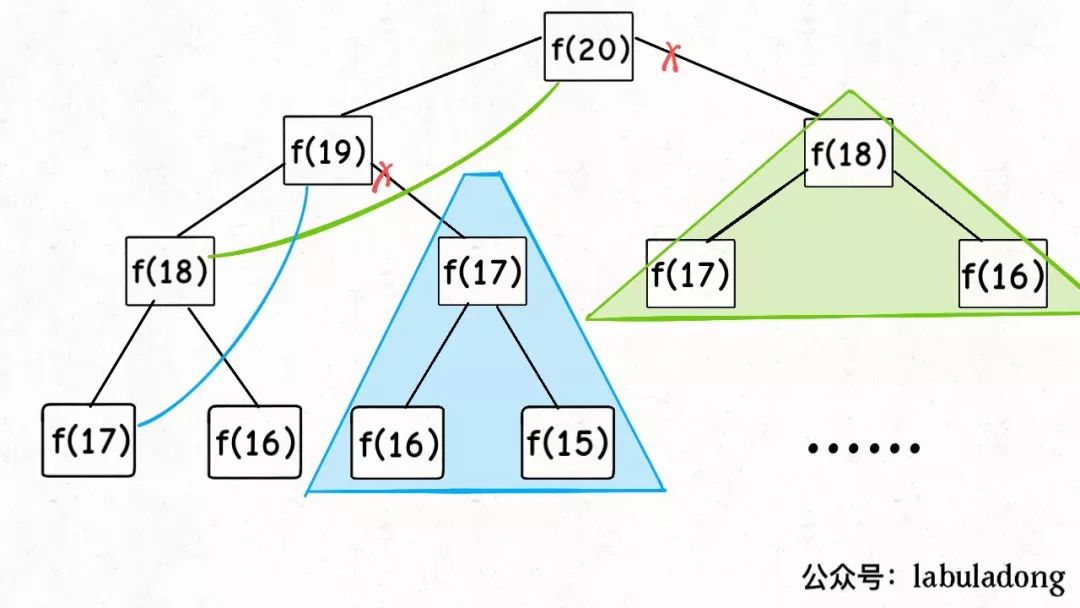
因此一个可行的办法是通过"备忘录"来剪枝, 如下图所示, 每次计算都放到了备忘录里, 那么再次遇到时直接从备忘录里取, 不需要重复计算一次了.

const memoize = (fn: Function) => {
  const cache = {}
  return (...args: number[]) => {
    const n = args[0]
    if (n in cache) {
      return cache[n]
    }

    const result = fn(n)
    cache[n] = result
    return result
  }
}

// 带备忘录的 fibonacci
export const fibonacci2 = memoize((n: number) => {
  if (n === 0 || n === 1) return n
  return fibonacci2(n - 1) + fibonacci2(n - 2)
})

dynamic-programming

具有动态规划雏形的斐波那契数列​

上面两种方式都是"自顶而下"的, 这道题反过来写, 即使用"自底而上"的思路也是 ok 的, 其状态转移方程如下, 那什么是状态转移方程呢? 你把 f(n) 想做一个状态 n, 这个状态 n 是由状态 n - 1 和状态 n - 2 相加转移而来, 这就叫状态转移.

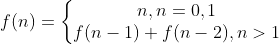
dynamic-programming 
export const fibonacci3 = (n: number) => {
  const dp = new Array(n + 1).fill(0)
  dp[1] = 1

  for (let i = 2; i <= n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2]
  }

  return dp[n]
}

当然由于求 n 的 fibonacci, 只关心 n 的前两个状态, 因此只要存储前两个即可. 因此最终求 fibonacci 时间复杂度最小为 O(n), 空间复杂度最小能为 O(1).

export function fibonacci4(n: number) {
  if (n <= 1) return n

  let prev = 0
  let curr = 1

  for (let i = 2; i <= n; i++) {
    const sum = prev + curr
    prev = curr
    curr = sum
  }
  return curr
}

动态规划的概念​

动态规划问题的一般形式就是求最值, 而求解解动态规划的核心思路是穷举. 因为要求最值, 肯定要把所有可行的答案穷举出来, 然后在其中找最值. 动态规划有三个特点:

  • DP 的穷举存在重叠子问题, 这些需要通过 memoize 或者 DP table 优化
  • DP 具备最优子结构, 通过子问题来求解最终问题, 注意子问题间必须互相独立
  • DP 需要列出正确的状态转移方程, 需要明确状态 -> 定义 dp 数组/函数的含义 -> 明确选择-> 明确 base case.

对于最有子结构, 有一个例子说的很好: 比如说, 你的原问题是考出最高的总成绩, 那么你的子问题就是要把语文考到最高, 数学考到最高... 为了每门课考到最高, 你要把每门课相应的选择题分数拿到最高, 填空题分数拿到最高... 当然, 最终就是你每门课都是满分, 这就是最高的总成绩. 这个过程符合最优子结构, 即每门科目考到最高这些子问题是互相独立, 互不干扰的.