归并排序

原理

归并排序是利用归并的思想实现的排序方法, 该算法采用经典的分治(divide-and-conquer)策略. 分治法将问题分(divide)成一些小的问题然后递归求解, 而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起, 即分而治之.

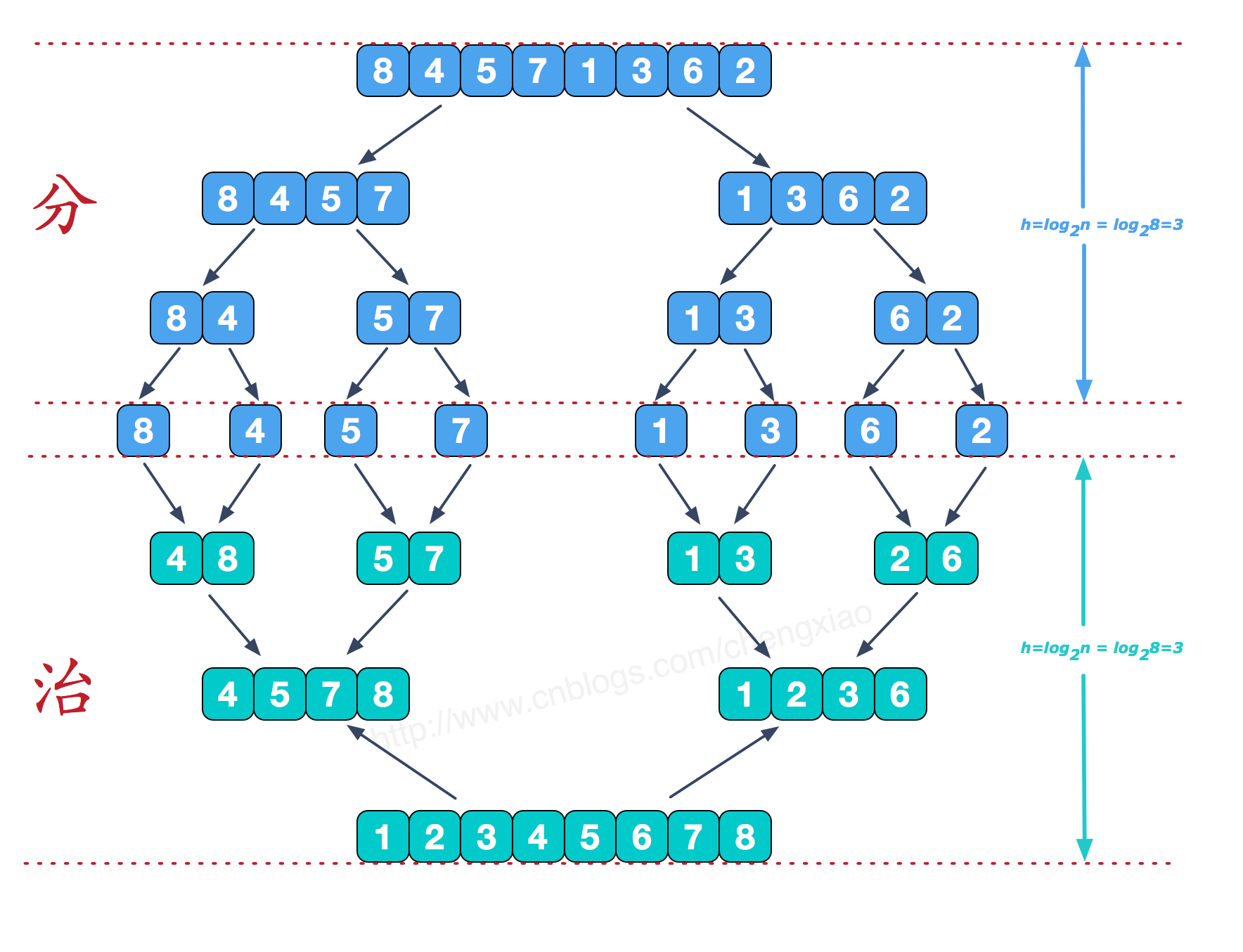
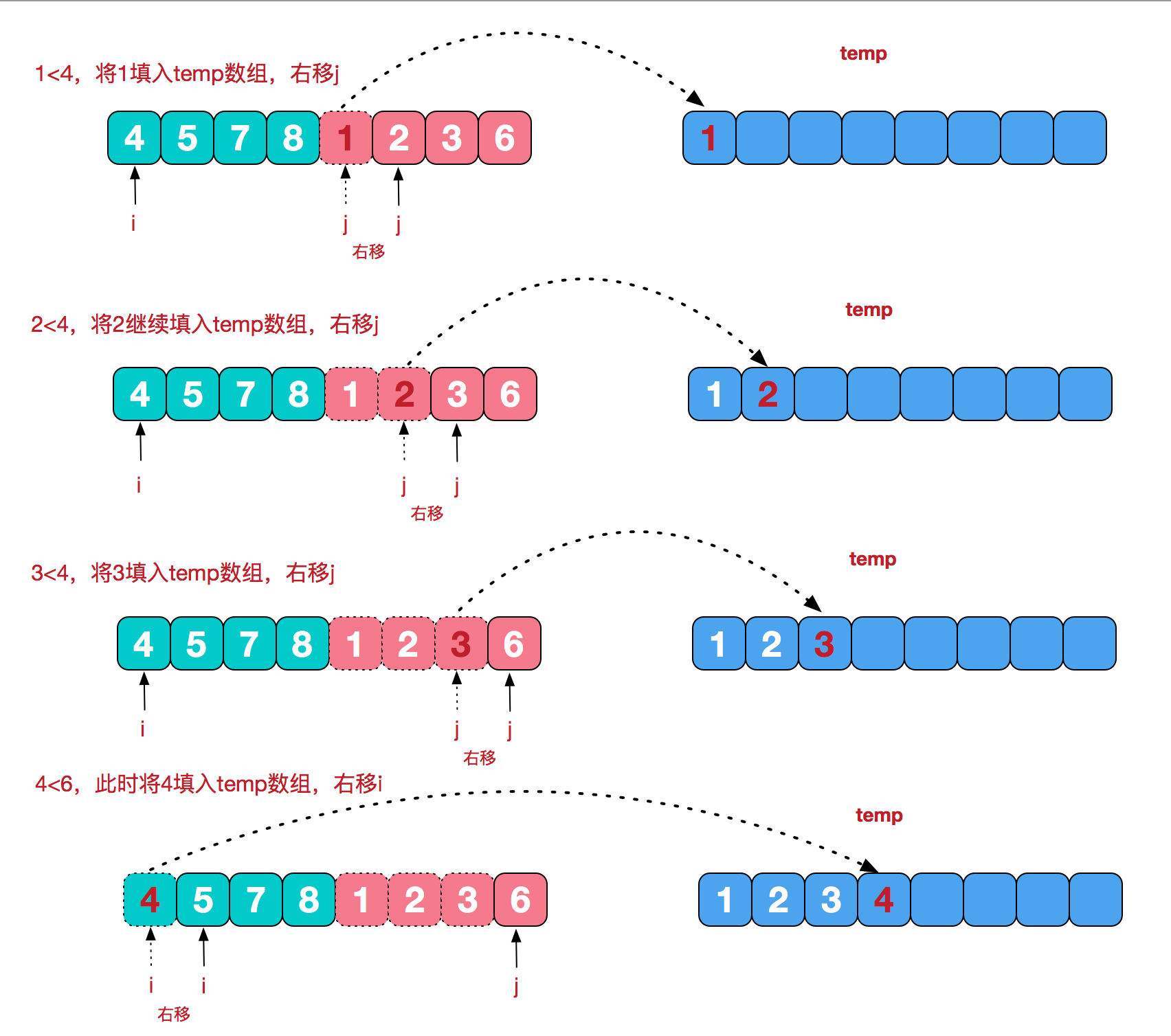
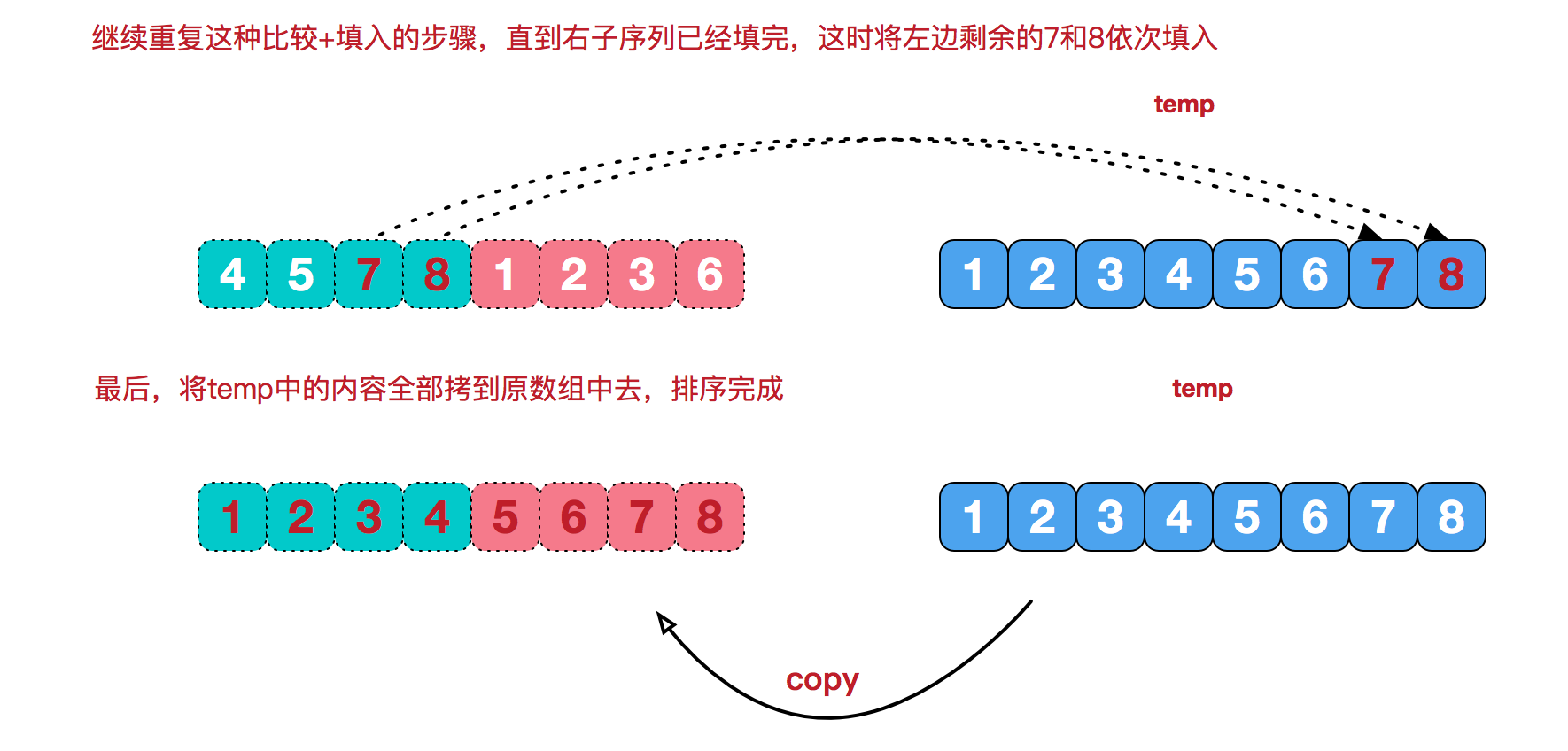
merge-sort

实现

export const merge = (
  arr: number[],
  left: number,
  mid: number,
  right: number,
  temp: number[],
) => {
  let i = left // 左序列指针
  let j = mid + 1 // 右序列指针
  let t = 0 // 临时数组指针
  while (i <= mid && j <= right) {
    if (arr[i] <= arr[j]) {
      temp[t++] = arr[i++]
    } else {
      temp[t++] = arr[j++]
    }
  }
  while (i <= mid) {
    // 将左边剩余元素填充进 temp 中
    temp[t++] = arr[i++]
  }
  while (j <= right) {
    // 将右序列剩余元素填充进 temp 中
    temp[t++] = arr[j++]
  }
  t = 0
  // 将 temp 中的元素全部拷贝到原数组中
  while (left <= right) {
    arr[left++] = temp[t++]
  }
}

export const sort = (
  arr: number[],
  left: number,
  right: number,
  temp: number[],
) => {
  if (left < right) {
    const mid = Math.floor((left + right) / 2)

    // ****** 分 ******/
    // 对数组的两部分分别排序
    sort(arr, left, mid, temp) // 左边归并排序, 使得左子序列有序
    sort(arr, mid + 1, right, temp) // 右边归并排序, 使得右子序列有序

    // ****** 治 ******/
    // 合并两个排好序的子数组
    merge(arr, left, mid, right, temp) // 将两个有序子数组合并操作
  }
}

export const mergeSort = (arr: number[]) => {
  const n = arr.length
  const temp = new Array<number>(n) // 在排序前, 先建好一个长度等于原数组长度的临时数组, 避免递归中频繁开辟空间
  sort(arr, 0, n - 1, temp)

  return arr
}

复杂度分析

归并排序是稳定排序, 它也是一种十分高效的排序, 能利用完全二叉树特性的排序一般性能都不会太差. java 中 Arrays.sort() 采用了一种名为 TimSort 的排序算法, 就是归并排序的优化版本. 从上文的图中可看出, 每次合并操作的平均时间复杂度为 O(n), 而完全二叉树的深度为 log2n. 总的平均时间复杂度为 O(nlogn). 而且, 归并排序的最好, 最坏, 平均时间复杂度均为 O(nlogn).

原理​

实现​

复杂度分析​

原理

实现

复杂度分析