不同的二叉搜索树

Tips

题目类型: Tree, Dynamic Programming

题目

给你一个整数 n, 求恰由 n 个节点组成且节点值从 1 到 n 互不相同的二叉搜索树有多少种? 返回满足题意的二叉搜索树的种数.

提示:

• 1 <= n <= 19

示例

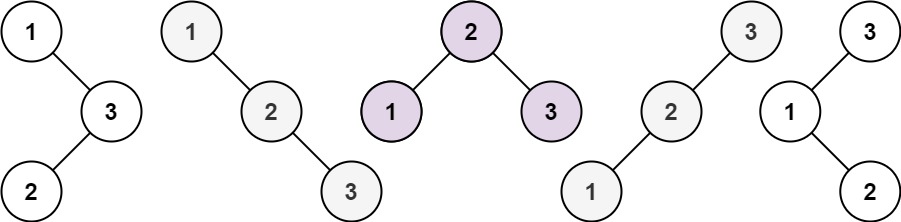
输入: n = 3
输出: 5

输入: n = 1
输出: 1

题解

二叉搜索树的特性是:

• 对于任意一个节点, 其左子树的所有节点值都小于该节点的值.
• 对于任意一个节点, 其右子树的所有节点值都大于该节点的值.

因此, 对于给定的 n, 我们可以选择 1 到 n 中的任何一个数 i 作为根节点. 那么:

• 值小于 i 的数 (1 到 i - 1) 将构成左子树.
• 值大于 i 的数 (i + 1 到 n) 将构成右子树.

因此, 我们遍历 1 到 n 的每个数 i 作为根节点. 对于每个 i:

• 左子树有 i - 1 个节点, 有 dp(i - 1) 种可能.
• 右子树有 n - i 个节点, 有 dp(n - i) 种可能.

因此以 i 为根的二叉搜索树有 dp(i - 1) * dp(n - i) 种可能.

/**
 * @param {number} n
 * @return {number}
 */
var numTrees = function (n) {
  const dp = new Array(n + 1).fill(0)
  dp[0] = 1 // 空树也是一种二叉搜索树
  dp[1] = 1 // 只有一个节点, 只有一种情况

  for (let i = 2; i <= n; i++) {
    for (let j = 1; j <= i; j++) {
      dp[i] += dp[j - 1] * dp[i - j]
    }
  }

  return dp[n]
}

• 时间复杂度: O(n²), 因为有两个嵌套循环.
• 空间复杂度: O(n), 用于存储 dp 数组.