不同路径

Tips

题目类型: Dynamic Programming

题目

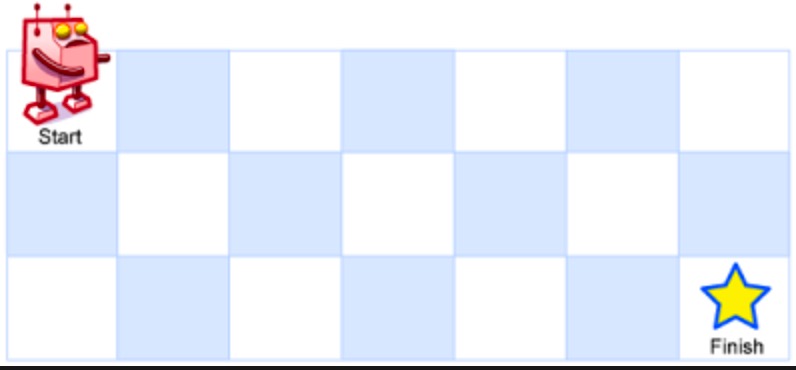
一个机器人位于一个 m * n 网格的左上角(起始点在下图中标记为 Start). 机器人每次只能向下或者向右移动一步. 机器人试图达到网格的右下角(在下图中标记为 Finish). 问总共有多少条不同的路径?

提示:

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 2 * 10ꝰ

示例

输入: m = 3, n = 7

输出: 28

题解

跟 64. 最小路径和 思路差不多, 具体看那道题. 由于每次转移只需要用到 dp[i - 1][j] 和 dp[i][j - 1], 因此空间压缩为一维.

JavaScript - 二维数组

/**
 * @param {number} m
 * @param {number} n
 * @return {number}
 */
var uniquePaths = function (m, n) {
  const dp = new Array(m).fill(0).map(() => new Array(n).fill(0))

  for (let i = 0; i < m; i++) {
    dp[i][0] = 1
  }

  for (let j = 0; j < n; j++) {
    dp[0][j] = 1
  }

  for (let i = 1; i < m; i++) {
    for (let j = 1; j < n; j++) {
      dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
    }
  }
  return dp[m - 1][n - 1]
}

JavaScript - 一维数组

/**
 * @param {number} m
 * @param {number} n
 * @return {number}
 */
var uniquePaths = function (m, n) {
  const dp = new Array(n).fill(1)
  for (let i = 1; i < m; i++) {
    for (let j = 1; j < n; j++) {
      dp[j] = dp[j] + dp[j - 1]
    }
  }
  return dp[n - 1]
}

Rust

pub fn unique_paths(m: i32, n: i32) -> i32 {
    let m = m as usize;
    let n = n as usize;
    let mut dp = vec![1; n];

    for i in 1..m {
        for j in 1..n {
            dp[j] = dp[j] + dp[j - 1];
        }
    }

    dp[n - 1]
}

复杂度分析

时间复杂度和空间复杂度都为 O(m * n)