n皇后-ii

Tips

题目类型: BackTracking

题目

n 皇后问题研究的是如何将 n 个皇后放置在 n * n 的棋盘上, 并且使皇后彼此之间不能相互攻击. 给你一个整数 n, 返回 n 皇后问题不同的解决方案的数量.

提示:

• 1 <= n <= 9

示例

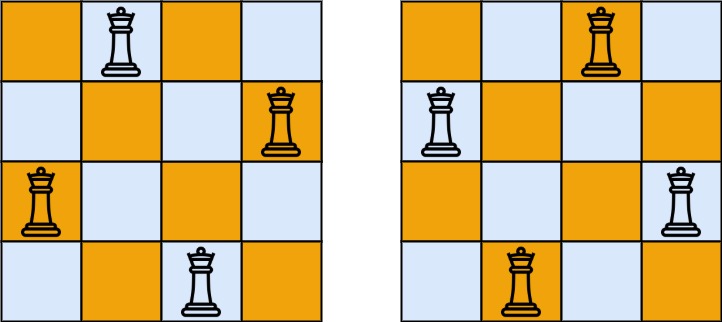
输入: n = 4

输出: 2

解释: 如上图所示, 4 皇后问题存在两个不同的解法.

题解

思路跟 51. n-皇后 没啥区别, 只过不这道题要求返回可行解的数量.

JavaScript

/**
 * @param {number} n
 * @return {number}
 */
var totalNQueens = function (n) {
  let count = 0
  const board = new Array(n).fill('').map(() => new Array(n).fill('.'))

  const dfs = (row) => {
    if (row === n) {
      count++
      return
    }

    for (let col = 0; col < n; col++) {
      if (!idValid(board, row, col)) continue

      board[row][col] = 'Q'
      dfs(row + 1)
      board[row][col] = '.'
    }
  }

  dfs(0)

  return count
}

/**
 * @param {string[][]} board
 * @param {number} row
 * @param {number} col
 * @return {number}
 */
var idValid = function (board, row, col) {
  const n = board.length

  for (let i = 0; i < row; i++) {
    if (board[i][col] === 'Q') return false
  }

  for (let i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
    if (board[i][j] === 'Q') return false
  }

  for (let i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
    if (board[i][j] === 'Q') return false
  }

  return true
}

Rust

#[allow(unused)]
pub fn total_n_queens(n: i32) -> i32 {
    let mut count = 0;
    let mut board = vec![vec!['.'; n as usize]; n as usize];

    dfs(&mut board, &mut count, 0);

    count
}

fn dfs(board: &mut Vec<Vec<char>>, count: &mut i32, row: usize) {
    let n = board.len();

    if row == n {
        // 由于这里的 count 是 &mut i32, 需要解引用成本体后再加一
        *count += 1;
        return;
    }

    for col in 0..n {
        if !is_valid(board, row, col) {
            continue;
        }

        board[row][col] = 'Q';
        dfs(board, count, row + 1);
        board[row][col] = '.';
    }
}

fn is_valid(board: &mut Vec<Vec<char>>, row: usize, col: usize) -> bool {
    let n = board.len();

    for i in 0..row {
        if board[i][col] == 'Q' {
            return false;
        }
    }

    let (mut i, mut j) = (row as i32 - 1, col as i32 + 1);
    while i >= 0 && j < n as i32 {
        if board[i as usize][j as usize] == 'Q' {
            return false;
        }

        i -= 1;
        j += 1;
    }

    let (mut i, mut j) = (row as i32 - 1, col as i32 - 1);
    while i >= 0 && j >= 0 {
        if board[i as usize][j as usize] == 'Q' {
            return false;
        }

        i -= 1;
        j -= 1;
    }

    true
}