Maximal Rectangle

Tips

Problem Type: Monotonic Stack

Problem

Given a rows x cols binary matrix filled with 0's and 1's, find the largest rectangle containing only 1's and return its area.

Constraints:

rows == matrix.length
cols == matrix[0].length
1 <= rows, cols <= 200
matrix[i][j] is '0' or '1'

Example

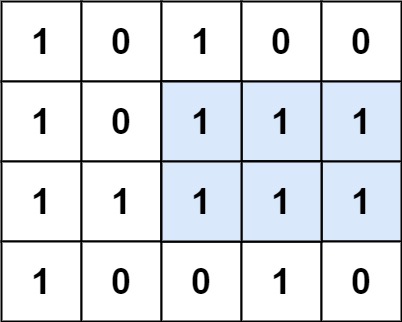
85-maximal-rectangle

Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]

Output: 6

Explanation: The maximal rectangle is shown in the above picture.

Solution

The key idea is to transform the 2D matrix into a series of histograms:

Using the last row as the base, we get heights as [4, 0, 0, 3, 0].

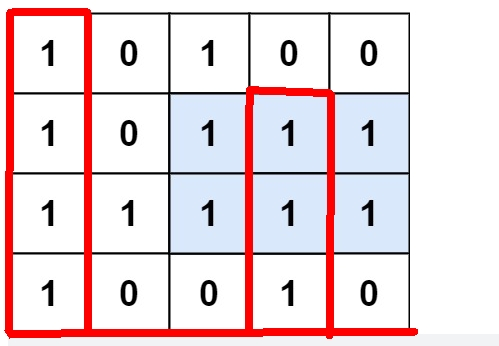
85-maximal-rectangle

Using the second to last row as the base, we get heights as [3, 1, 3, 2, 2].

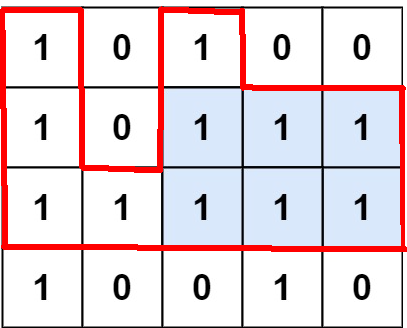
85-maximal-rectangle

By continuing this pattern, we generate multiple heights arrays. Then we can apply the approach from 84. Largest Rectangle in Histogram to calculate the maximum area for each heights array, and return the overall maximum.

JavaScript
Rust

/**
 * @param {character[][]} matrix
 * @return {number}
 */
var maximalRectangle = function (matrix) {
  const m = matrix.length
  const n = matrix[0].length

  const allHeights = []
  for (let i = m - 1; i >= 0; i--) {
    const heights = []

    for (let j = 0; j < n; j++) {
      let count = 0

      for (let k = i; k >= 0; k--) {
        if (matrix[k][j] === '1') {
          count++
        } else {
          break
        }
      }

      heights.push(count)
    }

    allHeights.push(heights)
  }

  let max = 0
  for (const heights of allHeights) {
    max = Math.max(max, largestRectangleArea(heights))
  }

  return max
}

/**
 * @param {number[]} heights
 * @return {number}
 */
var largestRectangleArea = function (heights) {
  const n = heights.length
  const left = new Array(n).fill(-1)
  const right = new Array(n).fill(n)
  const stack = []

  for (let i = 0; i < n; i++) {
    while (stack.length > 0 && heights[stack[stack.length - 1]] > heights[i]) {
      right[stack.pop()] = i
    }

    stack.push(i)
  }

  for (let i = n - 1; i >= 0; i--) {
    while (stack.length > 0 && heights[stack[stack.length - 1]] > heights[i]) {
      left[stack.pop()] = i
    }

    stack.push(i)
  }

  let max = 0

  for (let i = 0; i < n; i++) {
    const height = heights[i]
    const leftIdx = left[i]
    const rightIdx = right[i]
    max = Math.max(max, (rightIdx - leftIdx - 1) * height)
  }

  return max
}

use std::cmp;

pub fn maximal_rectangle(matrix: Vec<Vec<char>>) -> i32 {
    let m = matrix.len();
    let n = matrix[0].len();

    let mut all_heights = vec![];
    for i in (0..m).rev() {
        let mut heights = vec![];

        for j in (0..n) {
            let mut count = 0;

            for k in (0..=i).rev() {
                if matrix[k][j] == '1' {
                    count += 1;
                } else {
                    break;
                }
            }

            heights.push(count);
        }

        all_heights.push(heights);
    }

    let mut max = 0;

    for heights in all_heights {
        max = cmp::max(max, largest_rectangle_area(heights));
    }

    max
}

fn largest_rectangle_area(heights: Vec<i32>) -> i32 {
    let n = heights.len();
    let mut left: Vec<isize> = vec![-1; n];
    let mut right = vec![n; n];
    let mut stack = vec![];

    for i in 0..n {
        while !stack.is_empty() && heights[stack[stack.len() - 1]] > heights[i] {
            right[stack.pop().unwrap()] = i;
        }

        stack.push(i);
    }

    for i in (0..n).rev() {
        while !stack.is_empty() && heights[stack[stack.len() - 1]] > heights[i] {
            left[stack.pop().unwrap()] = i as isize;
        }

        stack.push(i);
    }

    let mut max = 0;
    for i in 0..n {
        let height = heights[i];
        let left_idx = left[i];
        let right_idx = right[i];
        max = cmp::max(max, height * (right_idx as i32 - left_idx as i32 - 1));
    }

    max
}

Problem​

Solution​

Problem

Solution