扰乱字符串

题目

使用下面描述的算法可以扰乱字符串 s 得到字符串 t:

1. 如果字符串的长度为 1, 算法停止
2. 如果字符串的长度大于 1, 执行下述步骤:
   • 在一个随机下标处将字符串分割成两个非空的子字符串. 即, 如果已知字符串 s, 则可以将其分成两个子字符串 x 和 y, 且满足 s = x + y.
   • 随机决定是要交换两个子字符串还是要保持这两个子字符串的顺序不变. 即, 在执行这一步骤之后, s 可能是 s = x + y 或者 s = y + x.
   • 在 x 和 y 这两个子字符串上继续从步骤一开始递归执行此算法.

给你两个长度相等的字符串 s1 和 s2, 判断 s2 是否是 s1 的扰乱字符串. 如果是, 返回 true; 否则, 返回 false.

提示:

• s1.length == s2.length
• 1 <= s1.length <= 30
• s1 和 s2 由小写英文字母组成

示例

输入: s1 = "great", s2 = "rgeat"
输出: true
解释: s1 上可能发生的一种情形是:
"great" --> "gr/eat" // 在一个随机下标处分割得到两个子字符串
"gr/eat" --> "gr/eat" // 随机决定: 保持这两个子字符串的顺序不变
"gr/eat" --> "g/r / e/at" // 在子字符串上递归执行此算法。两个子字符串分别在随机下标处进行一轮分割
"g/r / e/at" --> "r/g / e/at" // 随机决定: 第一组交换两个子字符串, 第二组保持这两个子字符串的顺序不变
"r/g / e/at" --> "r/g / e/ a/t" // 继续递归执行此算法, 将 "at" 分割得到 "a/t"
"r/g / e/ a/t" --> "r/g / e/ a/t" // 随机决定: 保持这两个子字符串的顺序不变
算法终止, 结果字符串和 s2 相同, 都是 "rgeat"
这是一种能够扰乱 s1 得到 s2 的情形, 可以认为 s2 是 s1 的扰乱字符串, 返回 true

输入: s1 = "abcde", s2 = "caebd"
输出: false

输入: s1 = "a", s2 = "a"
输出: true

题解

一开始看到随机, 还煞有介事的写了一堆 Math.random, 实际上可以理解为人家让你找出所有 s1 变换成扰乱字符串的形态, 只要有一个与 s2 相同, 就证明 s2 是 s1 的扰乱字符串.

JavaScript - 暴力递归

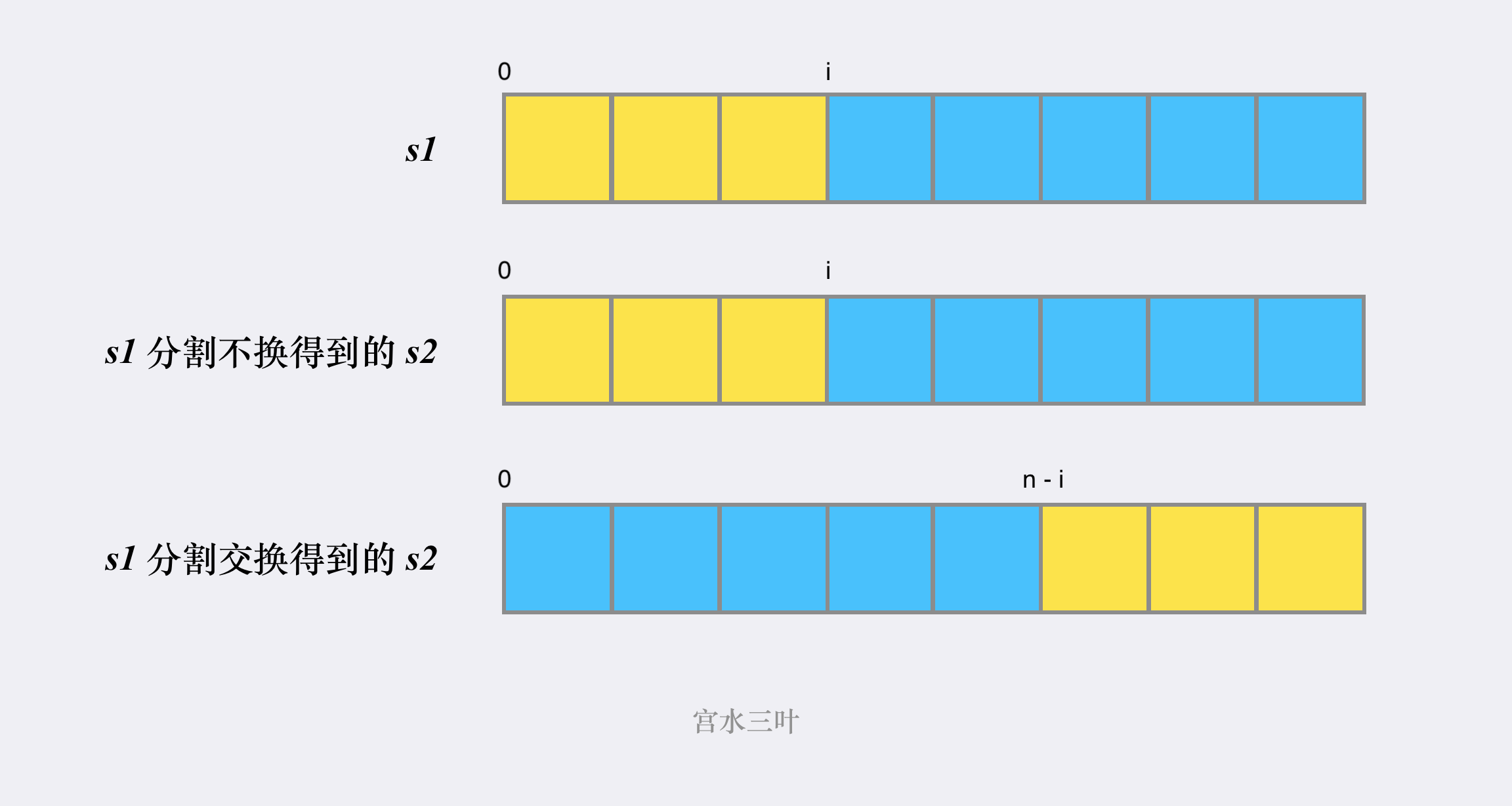
最朴素的是使用暴力递归, 中止条件要保证两个子字符串的长度相等, 且值相等. 然后分割 s1 和 s2 两个字符串, 由于 s2 可以被组装成 x + y 的形式, 也可能被组装成 y + x 的情况, 都需要考虑到.

/**
 * @param {string} s1
 * @param {string} s2
 * @return {boolean}
 */
var isScramble = function (s1, s2) {
  const dfs = (s1, s2) => {
    if (s1.length !== s2.length) return false
    if (s1 === s2) return true

    const n = s1.length
    for (let i = 1; i < n; i++) {
      // 按索引 i 切割 s1 字符串
      const x = s1.slice(0, i), // 黄色区域
        y = s1.slice(i) // 蓝色区域

      // 按索引 i 切割 s2 字符串, 不需要交换
      const a = s2.slice(0, i), // 黄色区域
        b = s2.slice(i) // 蓝色区域

      // 按索引 i 切割 s2 字符串, 需要交换
      const c = s2.slice(0, n - i), // 蓝色区域
        d = s2.slice(n - i) // 黄色区域

      if ((dfs(x, a) && dfs(y, b)) || (dfs(x, d) && dfs(y, c))) return true
    }

    return false
  }

  return dfs(s1, s2)
}

JavaScript - 记忆化搜索

扰乱不影响长度, 所以扰乱前的长度等于扰乱后的长度; 扰乱也不改变字符, 所以扰乱前的字符频次等于扰乱后的字符频次. 因此我们可以按着这个思路优化.

/**
 * @param {string} s1
 * @param {string} s2
 * @return {boolean}
 */
var isScramble = function (s1, s2) {
  const cache = new Map()

  const dfs = (s1, s2) => {
    if (s1.length !== s2.length) return false
    if (s1 === s2) return true

    // 扰乱前的字符频次等于扰乱后的字符频次, 如果不相等可以提前终止
    if (!check(s1, s2)) return false

    // 由于在暴力递归中会重复用到相同的 s1 和 s2, 这里记录一下, 作为记忆化 cache
    const key = s1 + '_' + s2
    if (cache.has(key)) return cache.get(key)

    const n = s1.length
    for (let i = 1; i < n; i++) {
      const x = s1.slice(0, i),
        y = s1.slice(i)

      const a = s2.slice(0, i),
        b = s2.slice(i),
        c = s2.slice(0, n - i),
        d = s2.slice(n - i)

      if ((dfs(x, a) && dfs(y, b)) || (dfs(x, d) && dfs(y, c))) {
        cache.set(key, true)
        return true
      }
    }

    cache.set(key, false)
    return false
  }

  return dfs(s1, s2)
}

/**
 * @param {string} s1
 * @param {string} s2
 * @return {boolean}
 */
const check = (s1, s2) =>
  // 这里受到第 49 题的启发, 可以通过给字符串按字母表排序来校验频次是否相等
  s1.split('').sort().join('') === s2.split('').sort().join('')

• 时间复杂度: O(n⁴)
• 空间复杂度: O(n³)

JavaScript - 动态规划

氛围烘托到这儿了, 不写个动态规划就说不过去了. dp[i][j][len] 代表 s1 从 i 开始, s2 从 j 开始, 后面长度为 len 的字符是否能形成扰乱字符串.

/**
 * @param {string} s1
 * @param {string} s2
 * @return {boolean}
 */
var isScramble = function (s1, s2) {
  if (s1 === s2) return true

  const n = s1.length
  const dp = new Array(n)
    .fill(false)
    .map(() => new Array(n).fill(false).map(() => new Array(n + 1).fill(false)))

  // 当 len 为 1, 只需比较两个字符相等即可
  for (let i = 0; i < n; i++) {
    for (let j = 0; j < n; j++) {
      dp[i][j][1] = s1[i] === s2[j]
    }
  }

  // 从 len > 1 开始遍历
  for (let len = 2; len <= n; len++) {
    // 遍历两个字符串
    for (let i = 0; i <= n - len; i++) {
      for (let j = 0; j <= n - len; j++) {
        // 分割
        for (let k = 1; k < len; k++) {
          // 对应了不发生交换
          const planA = dp[i][j][k] && dp[i + k][j + k][len - k]

          // 对应了发生了交换
          const planB = dp[i][j + len - k][k] && dp[i + k][j][len - k]

          if (planA || planB) {
            dp[i][j][len] = true
          }
        }
      }
    }
  }
  return dp[0][0][n]
}

• 时间复杂度: O(n⁴)
• 空间复杂度: O(n³)

Rust

use std::collections::HashMap;
 fn is_scramble(s1: String, s2: String) -> bool {
    let mut cache = HashMap::new();
    dfs(&s1, &s2, &mut cache)
}

fn dfs(s1: &str, s2: &str, cache: &mut HashMap<String, bool>) -> bool {
    if s1.len() != s2.len() {
        return false;
    }

    if s1 == s2 {
        return true;
    }

    if !check(&s1, &s2) {
        return false;
    }

    let key = s1.to_string() + "_" + s2;
    if let Some(x) = cache.get(&key) {
        return *x;
    }

    let n = s1.len();
    for i in 1..n {
        let (x, y) = (&s1[0..i], &s1[i..]);
        let (a, b) = (&s2[0..i], &s2[i..]);
        let (c, d) = (&s2[0..(n - i)], &s2[(n - i)..]);

        if (dfs(x, a, cache) && dfs(y, b, cache)) || (dfs(x, d, cache) && dfs(y, c, cache)) {
            cache.entry(key.to_string()).or_insert(true);
            return true;
        }
    }

    cache.entry(key.to_string()).or_insert(false);
    false
}

fn check(s1: &str, s2: &str) -> bool {
    let mut s1 = s1.split("").collect::<Vec<&str>>();
    s1.sort();
    s1.join("");

    let mut s2 = s2.split("").collect::<Vec<&str>>();
    s2.sort();
    s2.join("");

    s1 == s2
}