Largest Rectangle in Histogram

Tips

Problem Type: Monotonic Stack

Problem

Given an array of integers heights representing the histogram's bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.

Constraints:

1 <= heights.length <= 10⁵
0 <= heights[i] <= 10⁴

Examples

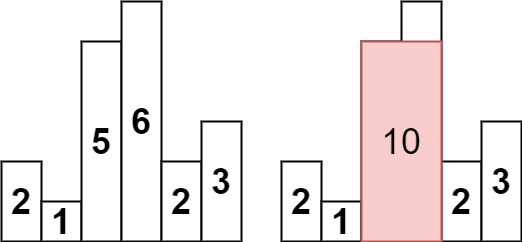
Input: heights = [2, 1, 5, 6, 2, 3]
Output: 10
Explanation: The largest rectangle is shown in the red area, which has an area of 10 units.

84-largest-rectangle-area

Input: heights = [2, 4]
Output: 4
Explanation: The largest rectangle is shown in the red area, which has an area of 4 units.

84-largest-rectangle-area

Solution

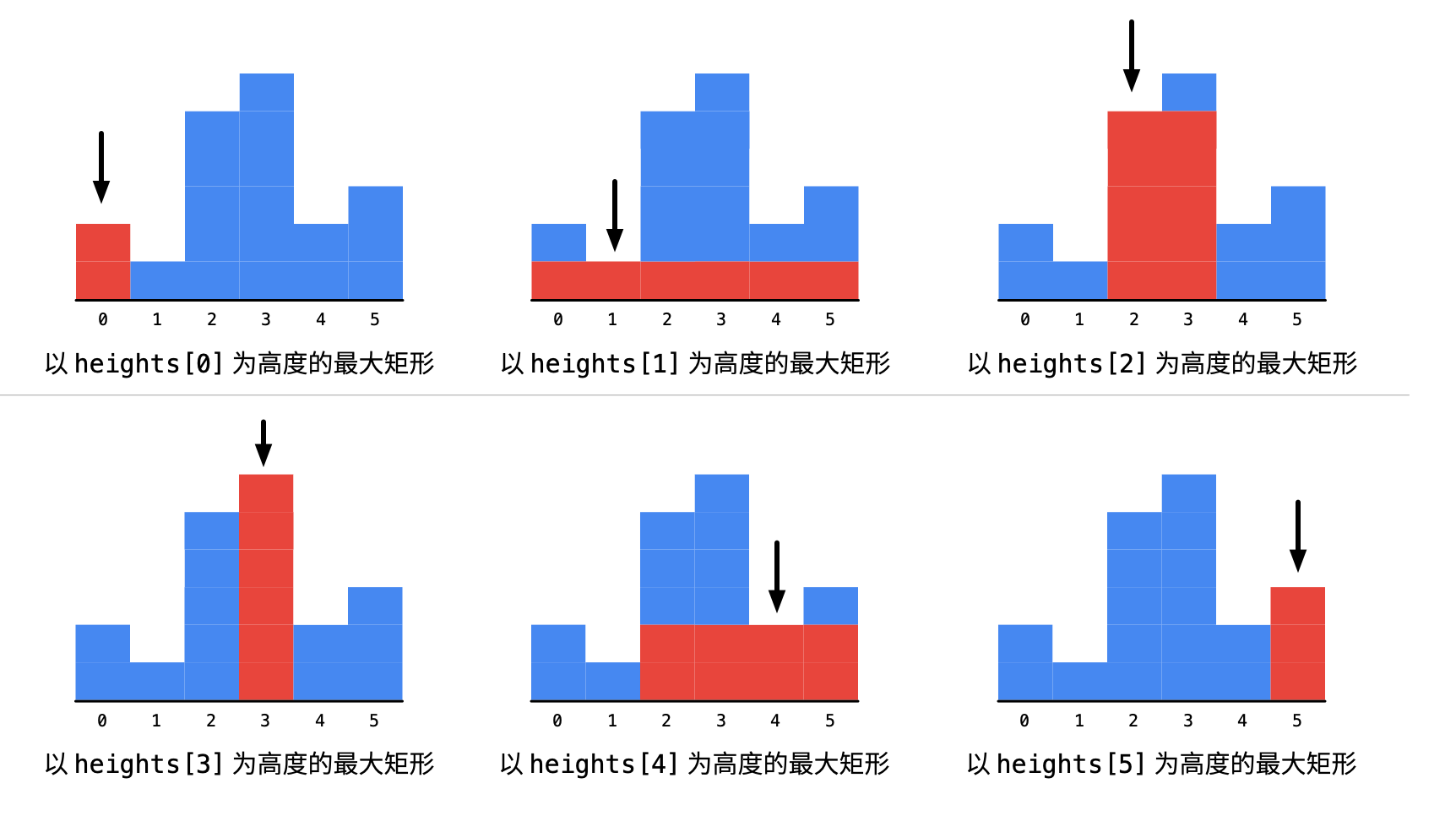
Whether using brute force or monotonic stack, the idea is to take a specific height, for example heights[2] (which is 5) in the first example, then expand in both directions to find the nearest bars that are shorter than it:

Expand left: heights[1] is less than heights[2], meaning to maintain the height of heights[2], the left boundary must be at index 1
Expand right: heights[4] is less than heights[2], meaning to maintain the height of heights[2], the right boundary must be at index 4

Thus, the maximum width maintaining the height heights[2] is 4 - 1 - 1 = 2.

84-largest-rectangle-area

For the brute force approach, we need to iterate through each height, then use it as a pivot and expand left and right to find the left and right boundaries. However, this results in O(n²) time complexity. Therefore, we can use a space-for-time strategy with a monotonic stack to pre-calculate the left and right boundaries for each bar. See the code comments for the specific implementation.

JavaScript - Brute Force
JavaScript - Monotonic Stack
Rust

/**
 * @param {number[]} heights
 * @return {number}
 */
var largestRectangleArea = function (heights) {
  const n = heights.length
  let max = 0

  for (let i = 0; i < n; i++) {
    const height = heights[i]

    let left = i
    while (left > 0 && heights[left - 1] >= height) {
      left--
    }

    let right = i
    while (right < n - 1 && heights[right + 1] >= height) {
      right++
    }

    max = Math.max(max, height * (right - left + 1))
  }

  return max
}

Time Complexity: O(n²)
Space Complexity: O(1)

/**
 * @param {number[]} heights
 * @return {number}
 */
var largestRectangleArea = function (heights) {
  const n = heights.length

  // Find the left boundary (smaller than current element) for each bar
  // Default is -1: if all elements to the left are taller,
  // we can extend the current height all the way to the left, so the boundary is -1
  //
  // Note: We use -1 instead of 0 because we're storing indices
  const lefts = new Array(n).fill(-1)

  // Find the right boundary (smaller than current element) for each bar
  // Default is n: if all elements to the right are taller,
  // we can extend the current height all the way to the right, so the boundary is n
  const rights = new Array(n).fill(n)

  const stack = []

  // Standard monotonic stack: find the right boundary (smaller element) for each bar
  for (let i = 0; i < n; i++) {
    while (stack.length > 0 && heights[stack[stack.length - 1]] > heights[i]) {
      rights[stack.pop()] = i
    }

    stack.push(i)
  }

  // Standard monotonic stack: find the left boundary (smaller element) for each bar
  for (let i = n - 1; i >= 0; i--) {
    while (stack.length > 0 && heights[stack[stack.length - 1]] > heights[i]) {
      lefts[stack.pop()] = i
    }

    stack.push(i)
  }

  let max = 0

  // Calculate the maximum area using left/right boundaries and current bar height
  for (let i = 0; i < n; i++) {
    max = Math.max(max, (rights[i] - lefts[i] - 1) * heights[i])
  }

  return max
}

Time Complexity: O(n)
Space Complexity: O(n)

use std::cmp;

pub fn largest_rectangle_area(heights: Vec<i32>) -> i32 {
    let n = heights.len();
    let mut left: Vec<isize> = vec![-1; n];
    let mut right = vec![n; n];
    let mut stack = vec![];

    for i in 0..n {
        while !stack.is_empty() && heights[stack[stack.len() - 1]] > heights[i] {
            right[stack.pop().unwrap()] = i;
        }

        stack.push(i);
    }

    for i in (0..n).rev() {
        while !stack.is_empty() && heights[stack[stack.len() - 1]] > heights[i] {
            left[stack.pop().unwrap()] = i as isize;
        }

        stack.push(i);
    }

    let mut max = 0;
    for i in 0..n {
        let height = heights[i];
        let left_idx = left[i];
        let right_idx = right[i];
        max = cmp::max(max, height * (right_idx as i32 - left_idx as i32 - 1));
    }

    max
}

Problem​

Solution​

Problem

Solution