编辑距离

Tips

题目类型: Dynamic Programming

相关题目:

• 10. 正则表达式匹配
• 44. 通配符匹配
• 115. 不同的子序列
• 516. 最长回文子序列
• 583. 两个字符串的删除操作
• 1143. 最长公共子序列

题目

给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数.

你可以对一个单词进行如下三种操作:

• 插入一个字符
• 删除一个字符
• 替换一个字符

提示:

• 0 <= word1.length, word2.length <= 500
• word1 和 word2 由小写英文字母组成

示例

输入: word1 = "horse", word2 = "ros"
输出: 3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

输入: word1 = "intention", word2 = "execution"
输出: 5
解释:
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

题解

对于一个单词, 我们有插入, 删除, 替换三种操作. 因此为了将 word1 转换成 word2:

• 在 word1 中插入一个字符等价于在 word2 中删除一个字符;
• 在 word2 中插入一个字符等价于在 word1 中删除一个字符.

因此, 对于 word1 的插入, 删除, 替换三种操作我们只需要考虑以下三种情况:

• word1 中删除一个字符;
• word2 中删除一个字符(等价于在 word1 中插入一个字符);
• word1 中替换一个字符.

因此定义二维数组 dp[i][j], 表示 word1 前 i 个字符和 word2 前 j 个字符的最小编辑距离.

考虑 word1 前 i 个字符和 word2 前 j 个字符的编辑距离, 在此之前:

• word1 前 i - 1 个字符已完成编辑, word2 前 j - 1 个字符已完成编辑, 所需最小编辑距离为 dp[i - 1][j - 1];
• word1 前 i - 1 个字符已完成编辑, word2 前 j 个字符已完成编辑, 所需最小编辑距离为 dp[i - 1][j];
• word1 前 i 个字符已完成编辑, word2 前 j - 1 个字符已完成编辑, 所需最小编辑距离为 dp[i][j - 1].

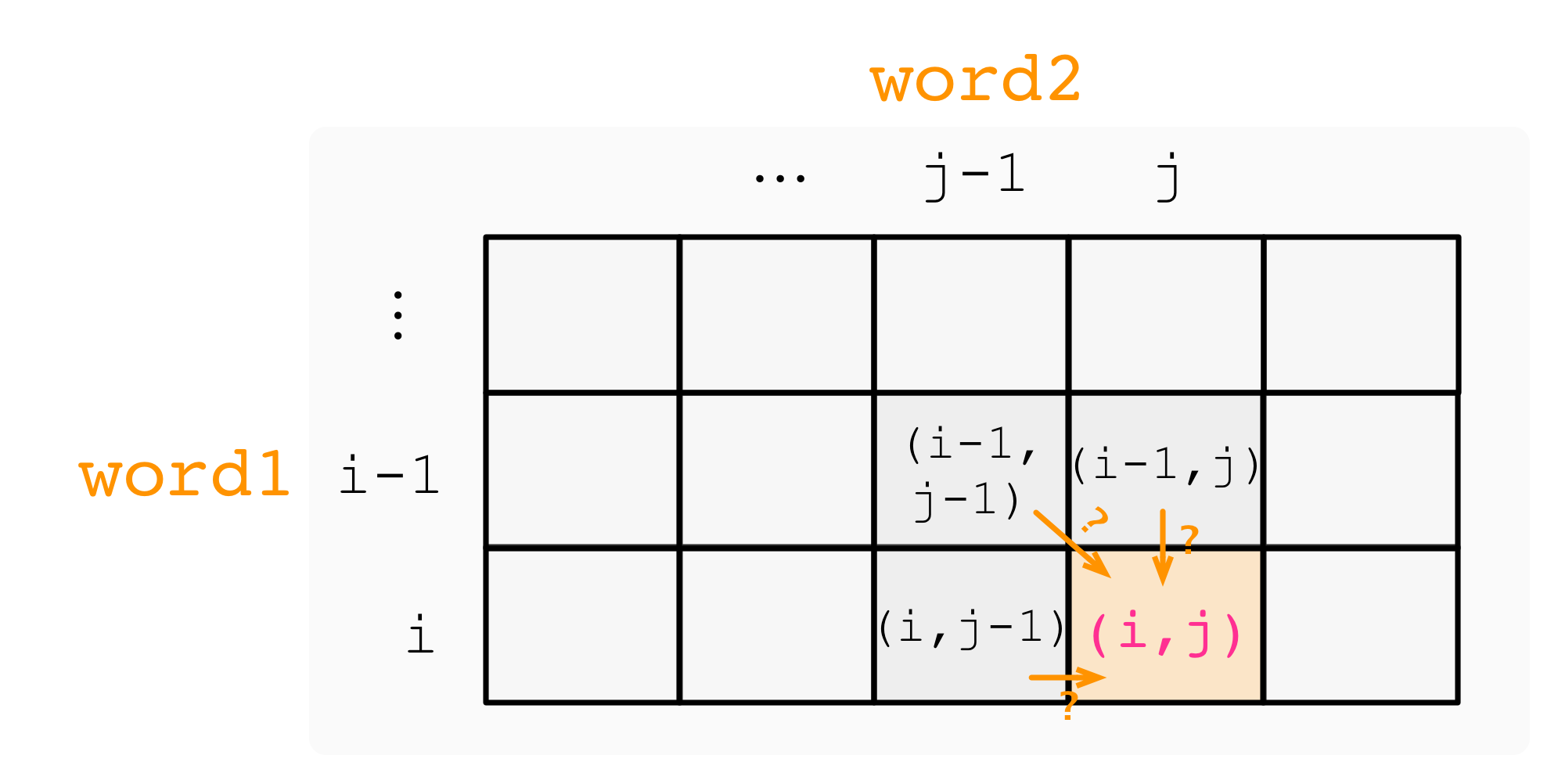
在进行状态转移的时候, 我们考虑 word1 第 i 个字符和 word2 第 j 个字符的匹配情况.

• 当 word1[i] === word2[j] 时, 有 dp[i][j] = dp[i - 1][j - 1].

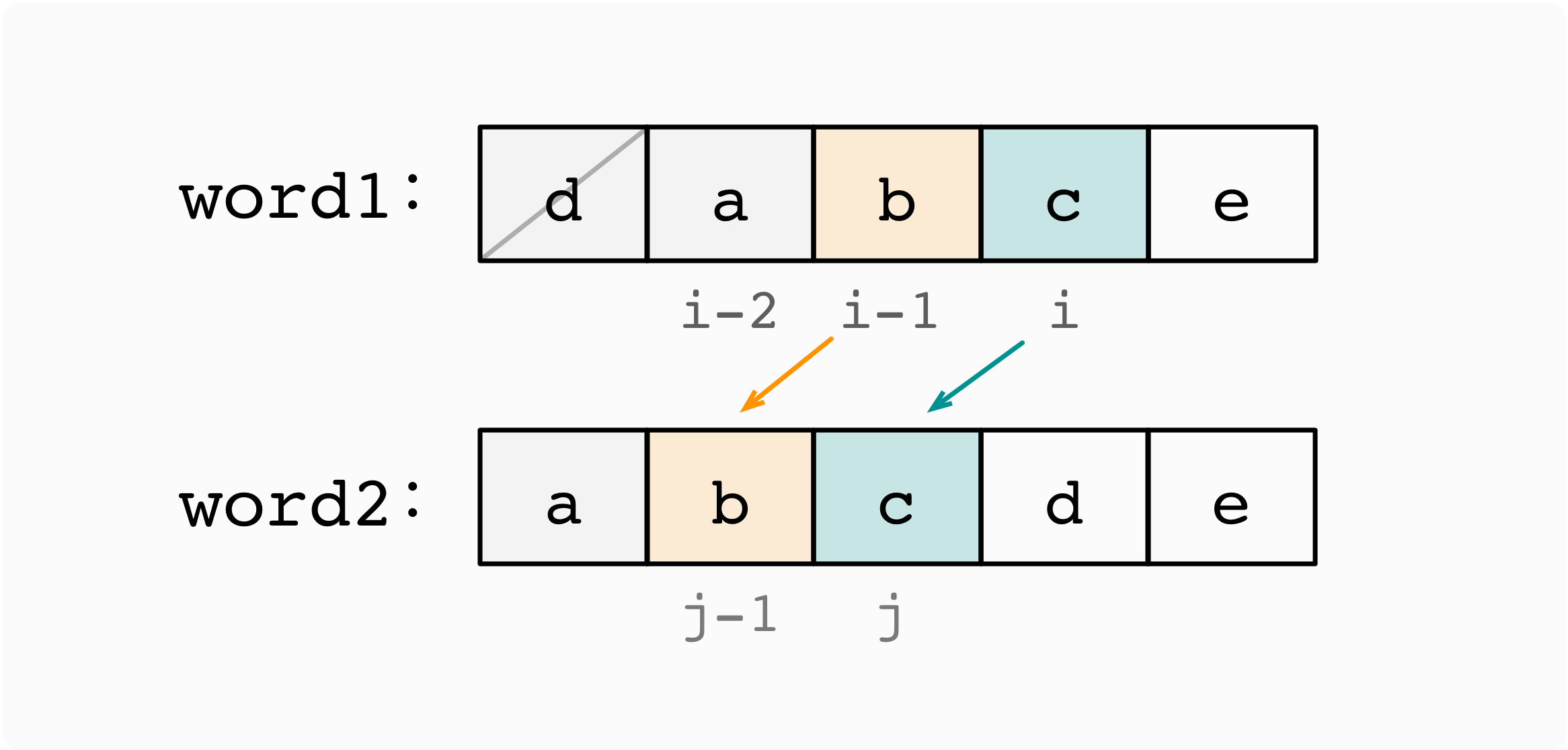
• 当 word1[i] !== word2[j] 时, 此时有三种情况:

  • word1 删除一个字符, 此时 dp[i][j] = dp[i - 1][j] + 1;
  • word2 删除一个字符, 此时 dp[i][j] = dp[i][j - 1] + 1;
  • word1 替换一个字符, 即将 word1[i] 替换为 word2[j], 此时 dp[i][j] = dp[i - 1][j - 1] + 1.

因此状态转移方程为:

• 当 word1[i] === word2[j], 有 dp[i][j] = dp[i - 1][j - 1];
• 当 word1[i] !== word2[j], 有 dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1

对于初始化 dp 数组, 显然

• dp[0][0] 为 0;
• dp[i][0] 为 i, 这是因为当 j 为 0 是, word2 前 j 个字符是个空字符串, 因此 word1 的前 i 个字符要想变成空字符串, 一定是要删除 i 次.
• dp[0][j] 为 j, 这是因为当 i 为 0 是, word1 前 i 个字符是个空字符串, 因此 word1 由空字符串变成 word2 前 j 个子字符串, 一定是要新增 j 次.

JavaScript

/**
 * @param {string} word1
 * @param {string} word2
 * @return {number}
 */
var minDistance = function (word1, word2) {
  const m = word1.length
  const n = word2.length
  const dp = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0))

  for (let i = 0; i <= m; i++) dp[i][0] = i
  for (let j = 0; j <= n; j++) dp[0][j] = j

  for (let i = 1; i <= m; i++) {
    for (let j = 1; j <= n; j++) {
      if (word1[i - 1] === word2[j - 1]) {
        dp[i][j] = dp[i - 1][j - 1]
      } else {
        dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1
      }
    }
  }

  return dp[m][n]
}

Rust

pub fn min_distance(word1: String, word2: String) -> i32 {
    let (word1, word2) = (word1.as_bytes(), word2.as_bytes());
    let (m, n) = (word1.len(), word2.len());
    let mut dp = vec![vec![0; n + 1]; m + 1];


    for i in 0..=m {
        dp[i][0] = i as i32;
    }

    for j in 0..=n {
        dp[0][j] = j as i32;
    }

    for i in 1..=m {
        for j in 1..=n {
            if word1[i - 1] == word2[j - 1] {
                dp[i][j] = dp[i - 1][j - 1];
            } else {
                dp[i][j] = cmp::min(dp[i - 1][j - 1], cmp::min(dp[i - 1][j], dp[i][j - 1])) + 1;
            }
        }
    }

    dp[m][n]
}