买卖股票的最佳时机-ii

Tips

题目类型: Dynamic Programming, Greedy

相关题目:

• 121. 买卖股票的最佳时机
• 123. 买卖股票的最佳时机-iii
• 188. 买卖股票的最佳时机-iv
• 309. 最佳买卖股票时机含冷冻期
• 714. 买卖股票的最佳时机含手续费

题目

给定一个数组, 它的第 i 个元素是一支给定股票第 i 天的价格. 设计一个算法来计算你所能获取的最大利润. 你可以尽可能地完成更多的交易(多次买卖一支股票). 注意: 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票).

示例

输入: [7,1,5,3,6,4]

输出: 7

解释: 在第 2 天(股票价格 = 1)的时候买入, 在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润为 5-1 = 4 . 随后, 在第 4 天(股票价格 = 3)的时候买入, 在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润为 6-3 = 3.

题解

JavaScript - 贪心

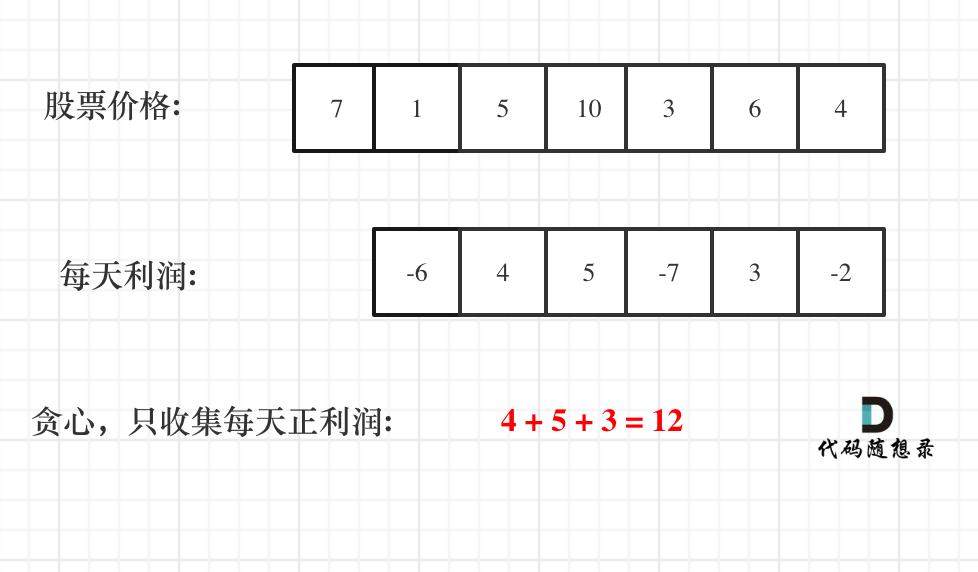
因为是可以多次买卖, 所以可以第一天买了第二天卖; 第二天买了第三天卖... 每次只取收益为正的, 最终就会得到最大收益.

/**
 * @param {number[]} prices
 * @return {number}
 */
var maxProfit = function (prices) {
  let max = 0
  for (let i = 1; i < prices.length; i++) {
    max += Math.max(prices[i] - prices[i - 1], 0)
  }

  return max
}

JavaScript - 动态规划

对于某一天 i, 要么是持有, 要么是不持有.

如果是持有:

• 这一天买入, 那么: dp[i][0] = dp[i - 1][1] - prices[i]
• 如果之前已经买入了, 那么: dp[i][0] = dp[i - 1][0]

如果是不持有:

• 这一天卖出, 那么: dp[i][1] = dp[i - 1][0] + prices[i]
• 之前已经卖出了, 那么: dp[i][1] = dp[i - 1][1]

/**
 * @param {number[]} prices
 * @return {number}
 */
var maxProfit = function (prices) {
  const n = prices.length
  const dp = new Array(n).fill(0).map(() => new Array(2).fill(0))

  dp[0][0] = -prices[0] // 第 0 天买入, 现金余额就是 -prices[0]
  dp[0][1] = 0 // 第 0 天卖出, 现金余额就是 0
  for (let i = 1; i < n; i++) {
    dp[i][0] = Math.max(dp[i - 1][1] - prices[i], dp[i - 1][0]) // 比起 121 题仅有的变化
    dp[i][1] = Math.max(dp[i - 1][0] + prices[i], dp[i - 1][1])
  }

  return dp[n - 1][1]
}