零钱兑换

Tips

题目类型: Dynamic Programming

相关题目:

• 518. 零钱兑换-ii(背包组合问题)

题目

给定不同面额的硬币 coins 和一个总金额 amount. 编写一个函数来计算可以凑成总金额所需的最少的硬币个数. 如果没有任何一种硬币组合能组成总金额, 返回 -1. 你可以认为每种硬币的数量是无限的.

示例

输入: coins = [1, 2, 5], amount = 11

输出: 3

解释: 1 + 5 + 5 = 11

题解

JavaScript

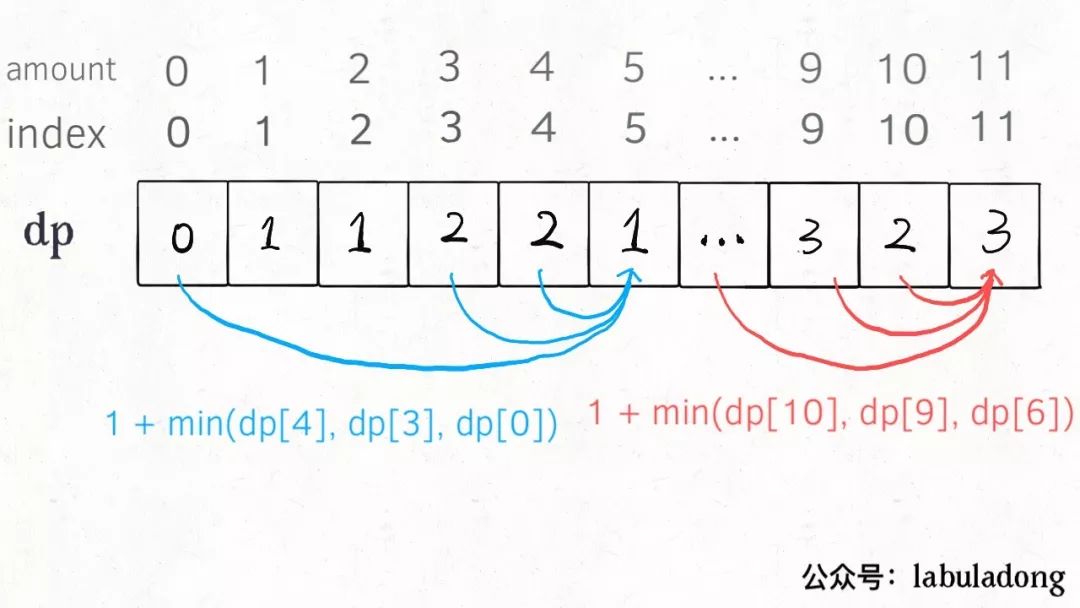
var coinChange = function (coins, amount) {
  const n = coins.length

  // 因为最低面值为 1, 所以组成金额 n 最多需要 n 枚硬币, 以此来代替 Infinite
  const dp = new Array(amount + 1).fill(amount + 1)

  // 凑足金额为 0 所需钱币的个数是 0
  dp[0] = 0

  for (let i = 0; i < n; i++) {
    for (let w = coins[i]; w <= amount; w++) {
      dp[w] = Math.min(dp[w], dp[w - coins[i]] + 1)
    }
  }

  return dp[amount] === amount + 1 ? -1 : dp[amount]
}

Rust

use std::cmp;

pub fn coin_change(coins: Vec<i32>, amount: i32) -> i32 {
    let n = coins.len();
    let mut dp = vec![amount + 1; (amount + 1) as usize];
    dp[0] = 0;

    for i in 0..n {
        for w in (coins[i] as usize)..=(amount as usize) {
            dp[w] = cmp::min(dp[w], dp[w - (coins[i] as usize)] + 1);
        }
    }

    if dp[amount as usize] == amount + 1 {
        -1
    } else {
        dp[amount as usize]
    }
}