插入区间

题目

给你一个无重叠的, 按照区间起始端点排序的区间列表. 在列表中插入一个新的区间, 你需要确保列表中的区间仍然有序且不重叠(如果有必要的话, 可以合并区间).

提示:

• 0 <= intervals.length <= 10⁴
• intervals[i].length == 2
• 0 <= intervals[i][0] <= intervals[i][1] <= 10⁴
• intervals 根据 intervals[i][0] 按升序排列
• newInterval.length == 2
• 0 <= newInterval[0] <= newInterval[1] <= 10⁴

示例

输入: intervals = [[1, 3], [6, 9]],  newInterval = [2, 5]
输出: [[1, 5], [6, 9]]

输入: intervals = [[1, 2], [3, 5], [6, 7], [8, 10], [12, 16]],  newInterval = [4, 8]
输出: [[1, 2], [3, 10], [12, 16]]
解释: 这是因为新的区间 [4, 8] 与 [3, 5], [6, 7], [8, 10] 重叠.

输入: intervals = [],  newInterval = [5, 7]
输出: [[5, 7]]

输入: intervals = [[1, 5]],  newInterval = [2, 3]
输出: [[1, 5]]

输入: intervals = [[1, 5]],  newInterval = [2, 7]
输出: [[1, 7]]

题解

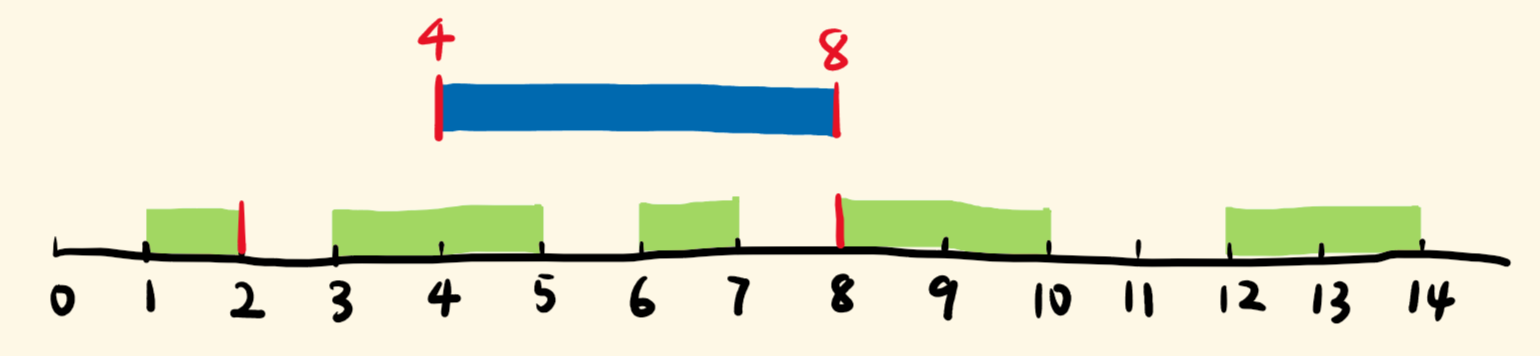
朴素思路就是三段式考虑, 以上图为例:

• intervals[i] 完全在 newInterval 的左侧
• intervals[i] 和 newInterval 有交叉
• intervals[i] 完全在 newInterval 的右侧

因此我们根据三种情况, 使用一个指针 i 在 intervals 游走:

• 首先会遇到 intervals[i][1] 完全在 newInterval 的左侧, 此时只需把 intervals[i] 放到新数组中即可
• 接着会遇到重叠部分, 看上图, 只要 intervals[i][0] <= newInterval[1], 就会发生重叠, 因此在这个条件下遍历, 左端取蓝绿左索引的较小者, 右端取蓝绿右索引的较大者, 来更新 newInterval, 这样在循环结束后, 就得到了合并区间, 然后放到新数组中即可
• 对于剩下的部分, 自然完全是在 newInterval 的右侧, 逐一放到新数组中即可

JavaScript

/**
 * @param {number[][]} intervals
 * @param {number[]} newInterval
 * @return {number[][]}
 */
var insert = function (intervals, newInterval) {
  const n = intervals.length
  const newIntervals = []
  let i = 0

  while (i < n && intervals[i][1] < newInterval[0]) {
    newIntervals.push(intervals[i])
    i++
  }

  while (i < n && intervals[i][0] <= newInterval[1]) {
    newInterval[0] = Math.min(newInterval[0], intervals[i][0])
    newInterval[1] = Math.max(newInterval[1], intervals[i][1])
    i++
  }
  newIntervals.push(newInterval)

  while (i < n) {
    newIntervals.push(intervals[i])
    i++
  }

  return newIntervals
}

Rust

use std::cmp;

pub fn insert(intervals: Vec<Vec<i32>>, new_interval: Vec<i32>) -> Vec<Vec<i32>> {
    let n = intervals.len();
    let mut new_interval = new_interval;
    let mut new_intervals = vec![];
    let mut i = 0;

    while i < n && intervals[i][1] < new_interval[0] {
        new_intervals.push(intervals[i].to_vec());
        i += 1;
    }

    while i < n && intervals[i][0] <= new_interval[1] {
        new_interval[0] = cmp::min(new_interval[0], intervals[i][0]);
        new_interval[1] = cmp::max(new_interval[1], intervals[i][1]);
        i += 1;
    }
    new_intervals.push(new_interval.to_vec());

    while i < n {
        new_intervals.push(intervals[i].to_vec());
        i += 1;
    }

    new_intervals
}