矩阵置零
题目
给定一个 m * n 的矩阵, 如果一个元素为 0, 则将其所在行和列的所有元素都设为 0, 请使用原地算法.
提示:
m == matrix.lengthn == matrix[0].length1 <= m, n <= 200-2³¹ <= matrix[i][j] <= 2³¹ - 1
进阶:
- 一个直观的解决方案是使用
O(m * n)的额外空间, 但这并不是一个好的解决方案. - 一个简单的改进方案是使用
O(m + n)的额外空间, 但这仍然不是最好的解决方案. - 你能想出一个仅使用常量空间的解决方案吗?
示例
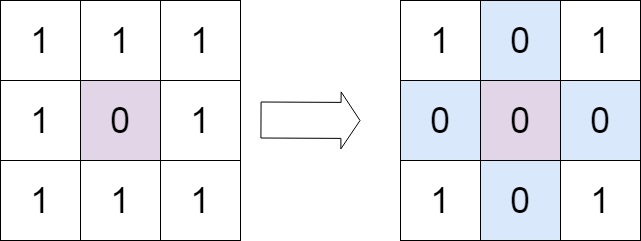
输入: matrix = [[1, 1, 1], [1, 0, 1], [1, 1, 1]]
输出: [[1, 0, 1], [0, 0, 0], [1, 0, 1]]
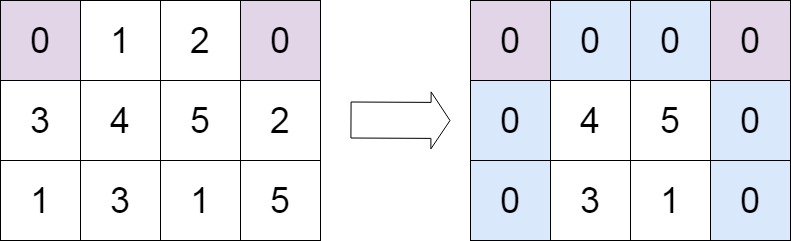
输入: matrix = [[0, 1, 2, 0], [3, 4, 5, 2], [1, 3, 1, 5]]
输出: [[0, 0, 0, 0], [0, 4, 5, 0], [0, 3, 1, 0]]
题解
- JavaScript - 两个线性变量
- JavaScript - 两个常数级变量
- Rust
朴素做法是创建 rows 和 cols 两个 HashSet, 遍历二维数组. 如果 matrix[i][j] 为 0,
把 i 和 j 分别存到 rows 和 cols 之中. 这样再次遍历时, 如果 i 或者 j 存在于 HashSet 中, 说明该元素所在的行或列存在 0, 那自然该元素也要变成 0.
/**
* @param {number[][]} matrix
* @return {void} Do not return anything, modify matrix in-place instead.
*/
var setZeroes = function (matrix) {
const m = matrix.length
const n = matrix[0].length
const rows = new Set()
const cols = new Set()
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (matrix[i][j] === 0) {
rows.add(i)
cols.add(j)
}
}
}
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (rows.has(i) || cols.has(j)) {
matrix[i][j] = 0
}
}
}
}
复杂度分析
- 时间复杂度:
O(m * n) - 空间复杂度:
O(m + n)
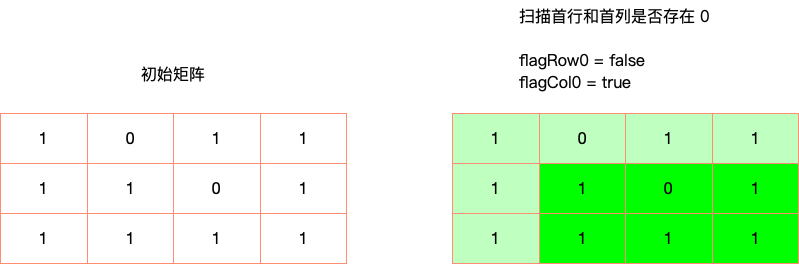
除了使用两个线性级的 HashSet, 也可以用两个常数级的变量 firstRowHasZero 和 firstColHasZero, 用于记录首行或者首列是否存在 0.
这样的目的是仅仅先记录首行和首列是否有 0, 而不去修改这两行, 因为一旦修改了, 其他行和列就算不准了.
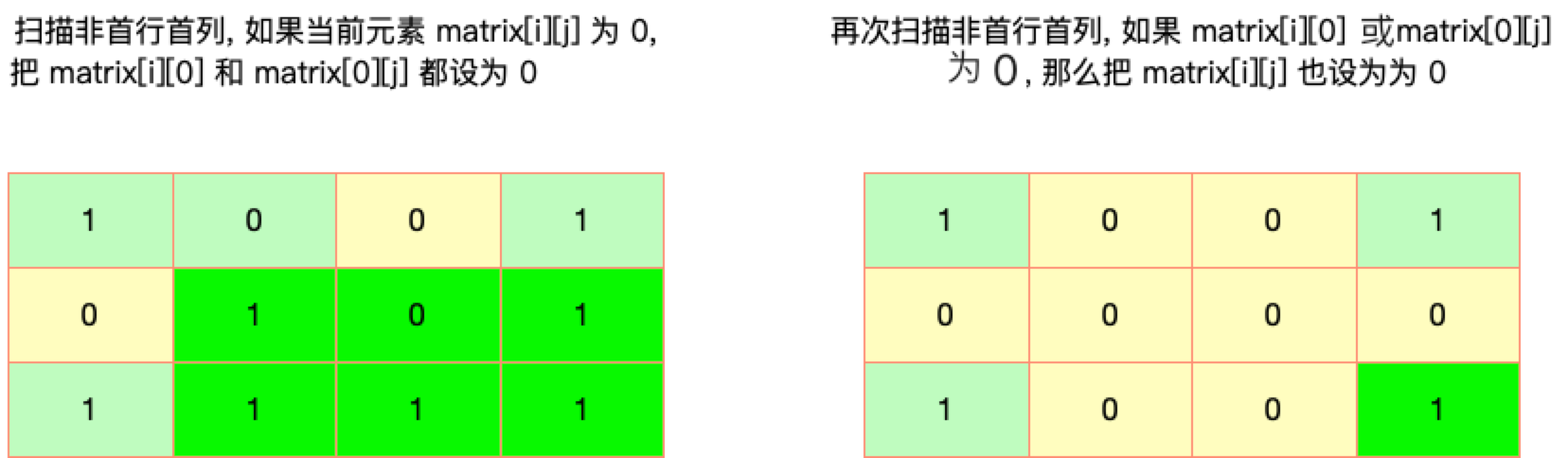
接下来扫描非首行首列, 如果当前元素 matrix[i][j] 为 0, 那么将对应的 matrix[i][0] 和 matrix[0][j] 设为 0, 这样做的目的是让首行首列来充当那两个 HashSet, 有效的减小了时间复杂度.
然后再次扫描非首行首列, 如果当前元素 matrix[i][j] 对应的 matrix[i][0] 或 matrix[0][j] 为 0, 说明该元素所在的行或列存在 0, 那么将该元素也设为 0.
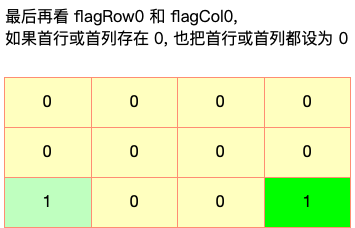
最后根据 firstRowHasZero 和 firstColHasZero 的情况将首行或首列都置为 0.
/**
* @param {number[][]} matrix
* @return {void} Do not return anything, modify matrix in-place instead.
*/
var setZeroes = function (matrix) {
const m = matrix.length
const n = matrix[0].length
let firstRowHasZero = false
let firstColHasZero = false
// 记录首行是否有 0
for (let i = 0; i < m; i++) {
if (matrix[i][0] === 0) {
firstRowHasZero = true
break // 找出一个 0 就行
}
}
// 记录首列是否有 0
for (let j = 0; j < n; j++) {
if (matrix[0][j] === 0) {
firstColHasZero = true
break // 找出一个 0 就行
}
}
// 扫描非首行 / 非首列
// 如果元素是 0, 将 matrix[i][0] 和 matrix[0][j] 设为 0
// 其实就相当于在首行 / 首列这两个 哈希表中注册对应的行 / 列是否有 0
for (let i = 1; i < m; i++) {
for (let j = 1; j < n; j++) {
if (matrix[i][j] === 0) {
matrix[i][0] = matrix[0][j] = 0
}
}
}
// 扫描非首行 / 非首列
// 如果哈希表对应的行 / 列是 0, 把该元素也抹零
for (let i = 1; i < m; i++) {
for (let j = 1; j < n; j++) {
if (matrix[i][0] === 0 || matrix[0][j] === 0) {
matrix[i][j] = 0
}
}
}
// 如果第一行有 0, 第一行抹零
if (firstRowHasZero) {
for (let i = 0; i < m; i++) {
matrix[i][0] = 0
}
}
// 如果第一列有 0, 第一列抹零
if (firstColHasZero) {
for (let j = 0; j < n; j++) {
matrix[0][j] = 0
}
}
}
复杂度分析
- 时间复杂度:
O(m * n) - 空间复杂度:
O(1)
pub fn set_zeroes(matrix: &mut Vec<Vec<i32>>) {
let m = matrix.len();
let n = matrix[0].len();
let mut flag_row_0 = false;
let mut flag_col_0 = false;
for i in 0..m {
if matrix[i][0] == 0 {
flag_row_0 = true;
break;
}
}
for j in 0..n {
if matrix[0][j] == 0 {
flag_col_0 = true;
break;
}
}
for i in 1..m {
for j in 1..n {
if matrix[i][j] == 0 {
matrix[i][0] = 0;
matrix[0][j] = 0;
}
}
}
for i in 1..m {
for j in 1..n {
if matrix[i][0] == 0 || matrix[0][j] == 0 {
matrix[i][j] = 0;
}
}
}
if flag_row_0 {
for i in 0..m {
matrix[i][0] = 0
}
}
if flag_col_0 {
for j in 0..n {
matrix[0][j] = 0
}
}
}