完全二叉树的节点个数

Tips

题目类型: Tree

题目

给你一棵完全二叉树的根节点 root, 求出该树的节点个数.

完全二叉树的定义如下: 在完全二叉树中, 除了最底层节点可能没填满外, 其余每层节点数都达到最大值, 并且最下面一层的节点都集中在该层最左边的若干位置. 若最底层为第 h 层, 则该层包含 1 ~ 2h 个节点.

示例

输入:

      1
    /  \
   2    3
 /  \   /
4   5  6

输出: 6

题解

暴力递归

最暴力的就写个递归, 这个方法不管你是什么二叉树, 一把梭, 把所有节点撸一遍, 返回总长度即可.

var countNodes = function (root) {
  return root !== null ? 1 + countNodes(root.left) + countNodes(root.right) : 0
}

最优解法

当然人家都说了是个完全二叉树, 不然只用暴力法就 too young, too simple, sometimes naive 了 🐸. 稍微复习下, 完美二叉树一定是完全二叉树, 但完全二叉树不一定是完美二叉树, 而完美二叉树可以用 2ⁿ - 1 直接算出总长度. 因此我们可以先判断是否为完美二叉树, 即如果最左线的高度等于最右线的高度, 证明是颗完美二叉树., 否则老老实实的走递归计算总长度.

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var countNodes = function (root) {
  let hLeft = 0,
    hRight = 0
  let pLeft = root,
    pRight = root

  while (pLeft) {
    ++hLeft
    pLeft = pLeft.left
  }
  while (pRight) {
    ++hRight
    pRight = pRight.right
  }

  // 如果最左线的高度等于最右线的高度, 证明是颗完美二叉树, 直接 2^n - 1 返回完活
  if (hLeft === hRight) return Math.pow(2, hLeft) - 1

  // 否则还是走递归那套
  return countNodes(root.left) + countNodes(root.right) + 1
}

复习各种二叉树

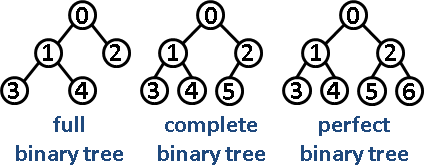
中文名	英文名	解释
完美二叉树	Perfect Binary Tree	Every node except the leaf nodes have two children and every level (last level too) is completely filled. 除了叶子结点之外的每一个结点都有两个孩子, 每一层(当然包含最后一层)都被完全填充.
完全二叉树	Complete Binary Tree	Every level except the last level is completely filled and all the nodes are left justified. 除了最后一层之外的其他每一层都被完全填充, 并且所有结点都保持向左对齐.
完满二叉树	Full/Strictly Binary Tree	Every node except the leaf nodes have two children. 除了叶子结点之外的每一个结点都有两个孩子结点.

• 完美(Perfect)二叉树一定是完全(Complete)二叉树, 但完全(Complete)二叉树不一定是完美(Perfect)二叉树.
• 完美(Perfect)二叉树一定是完满(Full)二叉树, 但完满(Full)二叉树不一定是完美(Perfect)二叉树.
• 完全(Complete)二叉树可能是完满(Full)二叉树, 完满(Full)二叉树也可能是完全(Complete)二叉树.
• 既是完全(Complete)二叉树又是完满(Full)二叉树也不一定就是完美(Perfect)二叉树.