Skip to main content

路径总和-iii

Tips

题目类型: Tree, 前缀和

相关题目:

题目​

给定一个二叉树的根节点 root, 和一个整数 targetSum, 求该二叉树里节点值之和等于 targetSum 的路径的数目.

路径不需要从根节点开始, 也不需要在叶子节点结束, 但是路径方向必须是向下的(只能从父节点到子节点).

示例

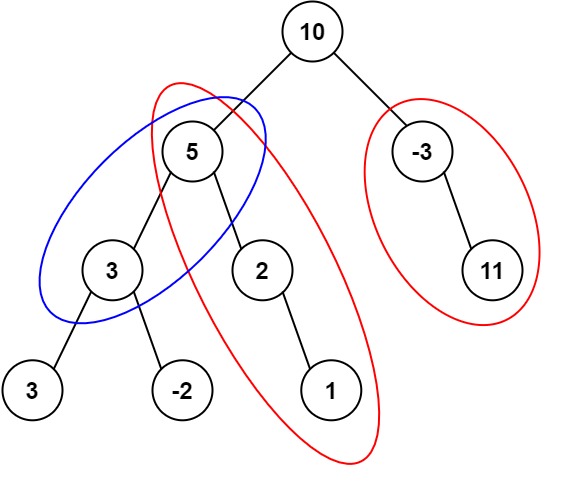
437-path-sum

输入: root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8

输出: 3

解释: 和为 8 的路径有三条

题解​

这道题可以通过前缀和的思路思考. 即从根节点 root 到某个子节点 node, 一定是唯一的路径(你可以把这条路径的所有元素想象成一个数组), 那么题目就变成了: 在这个数组中, 存在某个区间的和为 targetSum. 显然这就变成了一个前缀和的问题.

我们可以用一个 HasMap, key 记录前缀和, value 记录达成该前缀和包括的节点的个数. 具体解释看代码注释:

/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {number}
 */
var pathSum = function (root, targetSum) {
  const prefixSum = new Map()
  prefixSum.set(0, 1)
  let count = 0

  const dfs = (node, currentSum) => {
    if (!node) return

    currentSum += node.val

    if (prefixSum.has(currentSum - targetSum)) {
      count += prefixSum.get(currentSum - targetSum)
    }

    prefixSum.set(
      currentSum,
      prefixSum.has(currentSum) ? prefixSum.get(currentSum) + 1 : 1,
    ) // 回

    dfs(node.left, currentSum)
    dfs(node.right, currentSum)

    prefixSum.set(currentSum, prefixSum.get(currentSum) - 1) // 溯
  }

  dfs(root, 0)
  return count
}
  • 时间复杂度: O(n)
  • 空间复杂度: O(n)