组合总数

Tips

题目类型: BackTracking

题目

给你一个无重复元素的整数数组 candidates 和一个目标整数 target, 找出 candidates 中可以使数字和为目标数 target 的所有不同组合, 并以列表形式返回. 你可以按任意顺序返回这些组合.

candidates 中的同一个数字可以无限制重复被选取. 如果至少一个数字的被选数量不同, 则两种组合是不同的.

对于给定的输入, 保证和为 target 的不同组合数少于 150 个.

提示:

• 1 <= candidates.length <= 30
• 2 <= candidates[i] <= 40
• candidates 的所有元素互不相同
• 1 <= target <= 40

示例

输入: (candidates = [2, 3, 6, 7]), (target = 7)

输出: [[7], [2, 2, 3]]

输入: (candidates = [2, 3, 5]), (target = 8)

输出: [
  [2, 2, 2, 2],
  [2, 3, 3],
  [3, 5],
]

题解

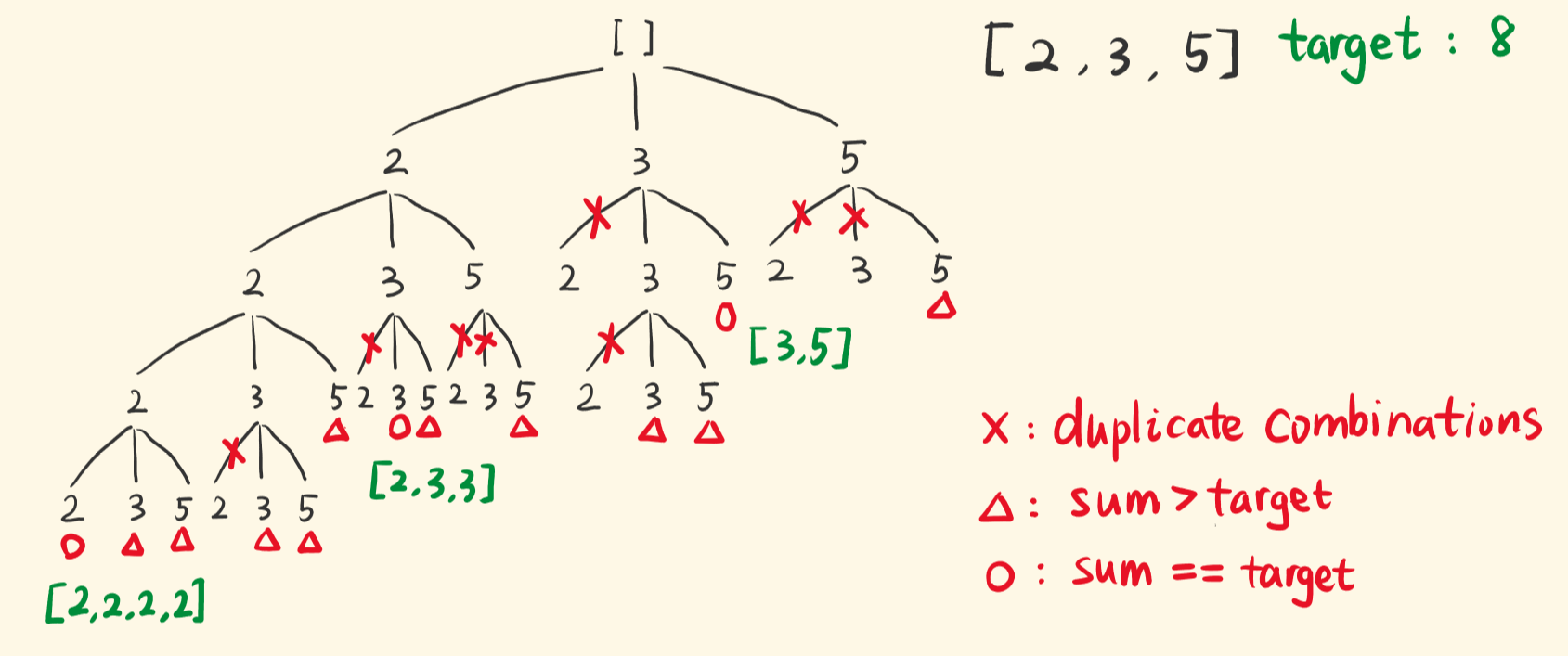
获取数字和为 target 的组合并不难, 即在每次递归探索时将已选列表的值累加, 然后将 sum === target 作为回溯的结束条件即可. 但是这样会导致组合重复, 比如 [2, 5] 和 [5, 2] 都会被输出.

因此我们需要对重复的部分进行剪枝, 只要限制下一次选择的起点, 是基于本次的选择, 这样下一次就不会选到本次选择的同层左边的数. 即通过控制 for 遍历的起点, 去掉会产生重复组合的选项.

JavaScript

/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum = function (candidates, target) {
  const n = candidates.length
  const res = []

  const dfs = (begin, sum, track) => {
    if (target === sum) {
      res.push(track)
      return
    }

    for (let i = begin; i < n; i++) {
      // 从 begin 开始选择
      if (sum < target) {
        track.push(candidates[i])

        // 基于当前这个数的继续选择, 传 i, 下一次就不会选到 i 左边的数
        dfs(i, sum + candidates[i], track.slice())

        // 撤销选择, 回到选择 candidates[i] 之前的状态, 继续尝试选同层右边的数
        track.pop()
      }
    }
  }

  dfs(0, 0, [])

  return res
}

Rust

pub fn combination_sum(candidates: Vec<i32>, target: i32) -> Vec<Vec<i32>> {
    let mut res: Vec<Vec<i32>> = vec![];
    dfs(0, 0, target, &candidates, &mut vec![], &mut res);
    res
}

fn dfs(
    begin: usize,
    sum: i32,
    target: i32,
    candidates: &Vec<i32>,
    track: &mut Vec<i32>,
    res: &mut Vec<Vec<i32>>,
) {
    if sum == target {
        res.push(track.to_vec());
        return;
    }

    for i in begin..candidates.len() {
        if sum < target {
            track.push(candidates[i]);
            dfs(i, sum + candidates[i], target, candidates, track, res);
            track.pop();
        }
    }
}