Skip to main content

交错字符串

Tips

题目类型: Dynamic Programming

题目​

给定三个字符串 s1, s2, s3, 请你帮忙验证 s3 是否是由 s1 和 s2 交错组成的. 要求使用 O(s2.length) 额外的内存空间来解决.

两个字符串 s 和 t 交错的定义与过程如下, 其中每个字符串都会被分割成若干非空子字符串:

  • s = s1 + s2 + ... + sn
  • t = t1 + t2 + ... + tm
  • |n - m| <= 1
  • 交错是 s1 + t1 + s2 + t2 + s3 + t3 + ... 或者 t1 + s1 + t2 + s2 + t3 + s3 + ...

注意: a + b 意味着字符串 a 和 b 连接.

提示:
  • 0 <= s1.length, s2.length <= 100
  • 0 <= s3.length <= 200
  • s1, s2, 和 s3 都由小写英文字母组成
示例

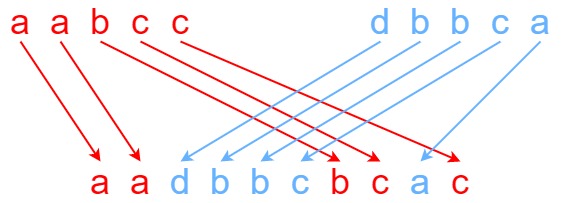
97-is-interleave

输入: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"

输出: true

题解​

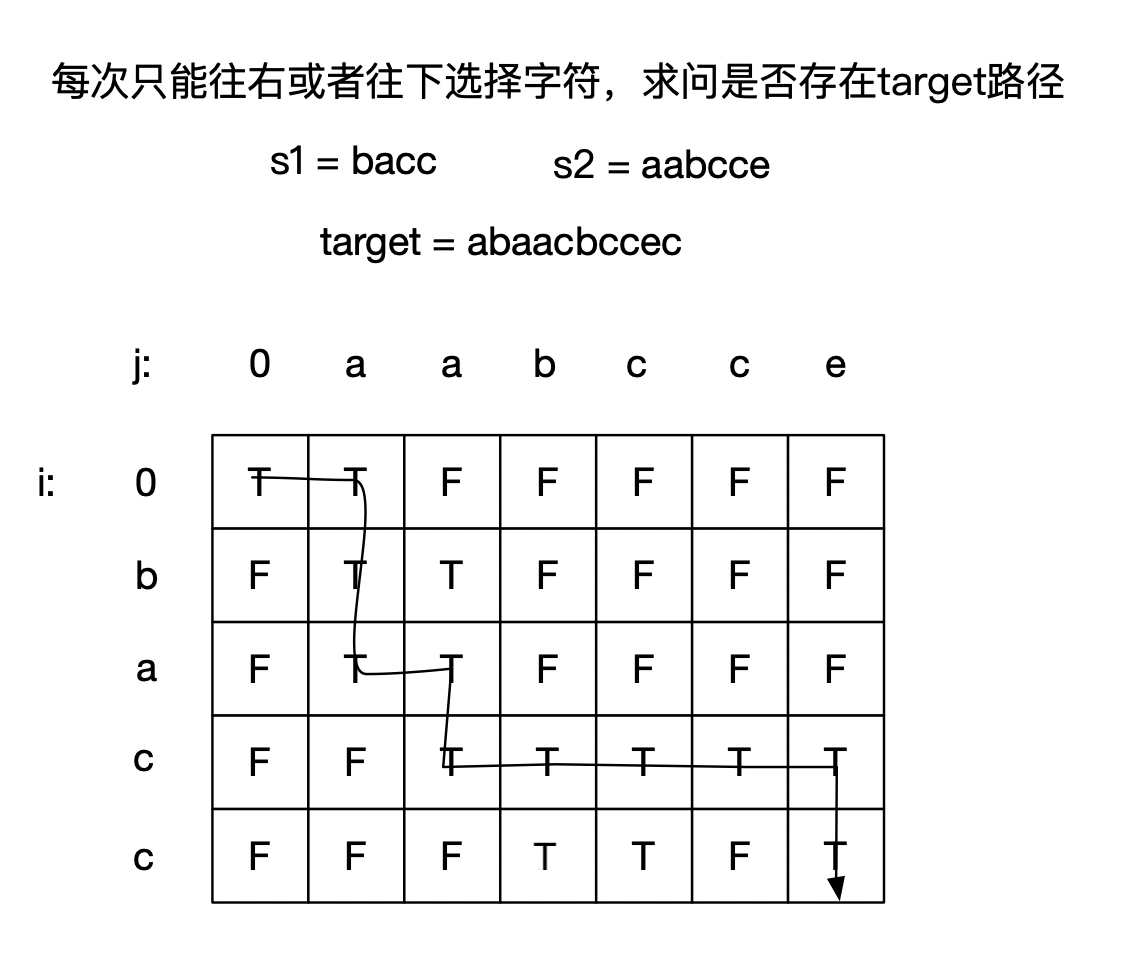
这道题如果能看出来可以转换成下面这种形态就好办了. 它就是 64. 最小路径和 的变种题, 即每次只能往右或往下选择字符, 是否存在路径可以从左上角到右下角.

97-is-interleave

于是可定义二维数组 dp, dp[i][j] 代表 s1 前 i 个字符与 s2 前 j 个字符拼接成 s3 的 i + j 个字符, 也就是存在目标路径能够到达 i, j.

状态转移方程:

  • dp[0][0] = true
  • 第一列只能一直往下走, 此时如果 s1[i - 1] === s3[i - 1], 有 dp[i][0] = true
  • 第一行只能一直往右走, 此时如果 s2[j - 1] === s3[j - 1], 有 dp[0][j] = true
  • 其他情况, 到达 dp[i][j] 可能由 dp[i - 1][j] 到达, 也可能由 dp[i][j - 1] 到达, 因此有 dp[i][j] = (dp[i - 1][j] && s1[i - 1] === s3[i + j - 1]) || (dp[i][j - 1] && s2[j - 1] === s3[i + j - 1])
/**
 * @param {string} s1
 * @param {string} s2
 * @param {string} s3
 * @return {boolean}
 */
var isInterleave = function (s1, s2, s3) {
  const m = s1.length
  const n = s2.length
  if (m + n !== s3.length) return false

  const dp = new Array(m + 1)
    .fill(false)
    .map(() => new Array(n + 1).fill(false))
  dp[0][0] = true

  for (let i = 1; i <= m && s1[i - 1] === s3[i - 1]; i++) dp[i][0] = true
  for (let j = 1; j <= n && s2[j - 1] === s3[j - 1]; j++) dp[0][j] = true
  for (let i = 1; i <= m; i++) {
    for (let j = 1; j <= n; j++) {
      dp[i][j] =
        (dp[i - 1][j] && s1[i - 1] === s3[i + j - 1]) ||
        (dp[i][j - 1] && s2[j - 1] === s3[i + j - 1])
    }
  }

  return dp[m][n]
}