最长递增子序列

Tips

Topics: Dynamic Programming, Binary Search

Similar Questions:

• 673. 最长递增子序列的个数

Description

Given an integer array nums, return the length of the longest strictly increasing subsequencee.

A subsequence is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.

Constraints:

• 1 <= nums.length <= 2500
• -10⁴ <= nums[i] <= 10⁴

Examples

Input: nums = [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.

Input: nums = [0,1,0,3,2,3]
Output: 4

Input: nums = [7,7,7,7,7,7,7]
Output: 1

Solution

JavaScript - Dynamic Programming

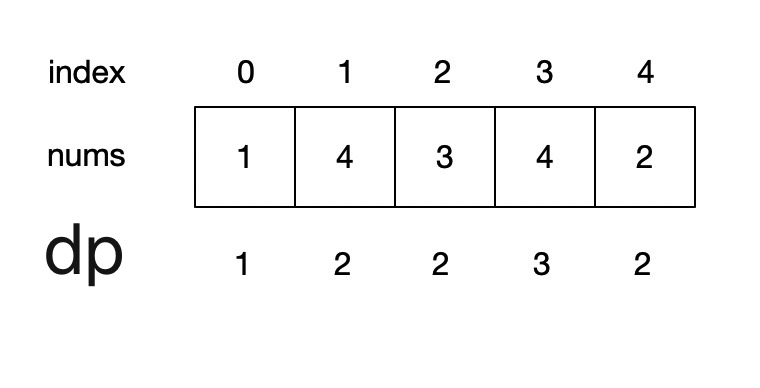
dp[i] 表示 i 之前包括 i 的以 nums[i] 结尾的最长递增子序列的长度, 位置 i 的最长升序子序列等于 j 从 0 到 i - 1 各个位置的最长升序子序列 + 1 的最大值.

/**
 * @param {number[]} nums
 * @return {number}
 */
var lengthOfLIS = function (nums) {
  const n = nums.length
  let max = 1
  const dp = new Array(n).fill(1)

  for (let i = 1; i < n; i++) {
    for (let j = 0; j < i; j++) {
      if (nums[j] < nums[i]) {
        dp[i] = Math.max(dp[i], dp[j] + 1)
      }
    }

    max = Math.max(max, dp[i])
  }

  return max
}

• Time complexity: O(n²).
• Space complexity: O(n).

JavaScript - Binary Search

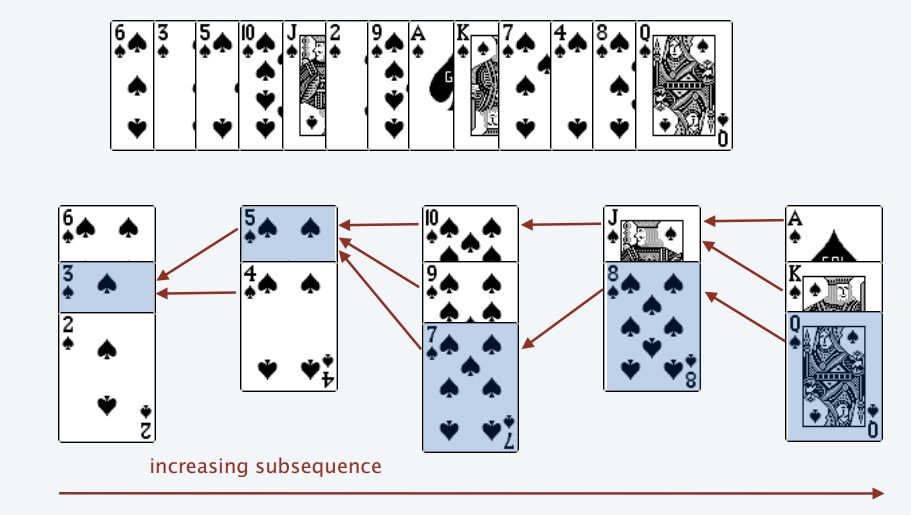
var lengthOfLIS = function (nums) {
  const n = nums.length
  const top = new Array(n)
  let piles = 0

  for (let i = 0; i < n; i++) {
    let pocker = nums[i]

    let left = 0,
      right = piles

    while (left < right) {
      const mid = Math.floor((left + right) / 2)

      if (top[mid] > pocker) {
        right = mid
      } else if (top[mid] < pocker) {
        left = mid + 1
      } else {
        right = mid
      }
    }

    if (left === piles) piles++
    top[left] = pocker
  }

  return piles
}

• Time complexity: O(nlogn).
• Space complexity: O(n).

Rust

use std::cmp;

pub fn length_of_lis(nums: Vec<i32>) -> i32 {
    let n = nums.len();
    let mut dp = vec![1; n];
    let mut max = 1;

    for i in 0..n {
        for j in 0..i {
            if nums[j] < nums[i] {
                dp[i] = cmp::max(dp[i], dp[j] + 1);
            }
        }

        max = cmp::max(max, dp[i]);
    }

    max
}